In material science and engineering, we always try to know more about the behaviour of a rigid body when it goes through stretching, twisting and squeezing. We make an effort to understand the behaviour of rigid bodies by establishing a relation between applied force and deformation. So, to understand the mechanical properties of a substance, we must first understand the answer to the question- “what is stress?”
Meaning of stress
Stress is defined as the internal restoring force of an object per unit area. Let us take an example. If we apply force on a rubber wire, it elongates. After a while, when we remove the force, the rubber regains its original shape and size.
Now, the question is: what is the responsible force which drives back the rubber to its original position?
An internal force is developed when we apply the external force. The magnitude of this restoring force increases as the elongation of wire increases. When we remove the external force, the rubber wire returns to its original shape and size due to restoring force. So, stress is the restoring force per unit area that acts inside the body.
Formula for stress
Mathematically, we can represent stress as:

where,
is stress
F is the restoring force
A is the surface area to which F is perpendicular
Some important points about stress
- Stress is a tensor quantity.
- Its dimension is [M¹L-¹T-²]
- In the SI system, the unit of stress is Nm-² or Pascal. But, this unit of stress is very small. So, in engineering applications, some larger units like MPa, GPa are used.
1MPa=106Pa=1N/mm²
1GPa=1000MPa=1KN/mm²
Types of stress
In a border sense, we can classify stress as:
Simple or Direct Stress:
Simple or direct stress can be defined as the stress produced due to direct loading. For example, when a heavy mass is suspended by a rod.
Three types of stress are considered direct or simple stress.
- Tension
- Compression
- Shear
Indirect Stress:
When a load is applied on a body and the body is deformed, due to that deformation, stress is produced. This is called indirect stress.
Let us understand these stresses in more detail.
- Tensile and Compressive Stress: Tensile or compressive stress is simply the applied force perpendicular per unit area. Tensile stress is defined for tension force whereas compressive stress is defined for compressive force.
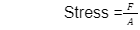
Where F is the magnitude of the force acting tangential to the surface having area A.
- Volumetric Stress: If we apply force on the total volume of a body, the pressure force per unit area on it is called volumetric stress.
- Bending Stress: When a load is applied perpendicular to the axis of a body or a couple of forces acting in a plane passing through the axis, it causes bending. The stress developed due to this bending is called bending stress.
What is stress? Questions
Question 1: In the given figure, forces on each cross-section are shown. The surface areas of the cross-sections are:
Area of AB=Area of CD=2mm², Area of EF= Area of GH=1mm².
Then, find the stress on the surface AB and GH.
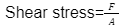
where F is the magnitude of the force, perpendicular to the area, A.
- Shear Stress: Shear stress is also force per unit area but here the force vector is not perpendicular to the surface; it lies on the plane of area. Shear stress=FA
Where F is the magnitude of the force acting tangential to the surface having area A.
- Volumetric Stress: If we apply force on the total volume of a body, the pressure force per unit area on it is called volumetric stress.
- Bending Stress: When a load is applied perpendicular to the axis of a body or a couple of forces acting in a plane passing through the axis, it causes bending. The stress developed due to this bending is called bending stress.
What is stress? Questions
Question 1: In the given figure, forces on each cross-section are shown. The surface areas of the cross-sections are:
Area of AB=Area of CD=2mm², Area of EF= Area of GH=1mm².
Then, find the stress on the surface AB and GH.

Solution:
- i) If we analyse from the left side, then, the net force on the left side of AB =50+20=70N
Hence total load on either side of AB=70N
The surface area of AB= 2mm²
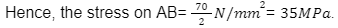
- Similarly, the net force on the right side of GH= 40 N.
As the rod is in equilibrium then we can say that the total force on either side of the surface GH= 40 N
Surface area GH= 1mm²
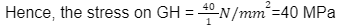
Question 2: A balloon is filled with air having an internal pressure of 3Pa. The diameter of the balloon is 4cm. Then find the volumetric stress.
Solution:
As the balloon is in equilibrium, its volume is constant. Then, the total force on either side of the surface is the same. The pressure is equal to the volumetric stress here.
Hence, volumetric stress = 3Pa
Question 3: A rod having uniform mass 5 kg, cross-section area 2m² and length 2 m. Find the stress at 1 m height above the bottom part, if it suspended vertically from a wall
Solution:
As the rod is suspended vertically, the force is acting on it due to its weight at the centre of mass of the rod.
Given,
Mass of the rod = M= 5 kg
Area of cross section = A= 2 m²
So, force on rod = weight of the rod =mg=510=50N
Hence, stress at 1 m height above the bottom part = stress at COM = 50/2=25 Pa.
Conclusion
In material engineering and science, there are various studies and applications of stress. With the information of stress on a body, we can calculate the elongation produced on the body. When the stress on a material increases, various changes take place, which can be explained using stress-strain diagrams. By using Hooke’s law, we can derive elastic constants from stress.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






