Profile
Settings
Refer your friends
Sign out
The sandwich theorems are otherwise called the Squeeze theorem Pinch theorem. This is utilized to extrapolate the worth of a function at a point x by involving two functions in the area. There is additionally an intriguing account related to the sandwich theorem. It expresses that there are two cops accompanying an alcoholic. Both these police officers enter a cell, then, at that point, no matter what the way that the alcoholic is wobbling, he should enter the cell as well. This is the way this theorem is utilized. Allow us to check its assertion out.
The ham sandwich theorem says that assuming there are three solids in space, a plane exists that divides everyone into two sections with equivalent volumes. Consider two cuts of bread and a cut of ham, however, they could be anyplace in space.
Sandwich Theorem – Let p, q and r be three capacities having the very area to such an extent that p(x) ≤ q(x) ≤ r(x). For a genuine number ‘a’ on the off chance thatxap(x) = xaq(x) = l, xa r(x) should be equivalent to 1.
This is shown. Allow us to check out at the verification utilizing a model.
Demonstrate that cosx < sinx/x <1
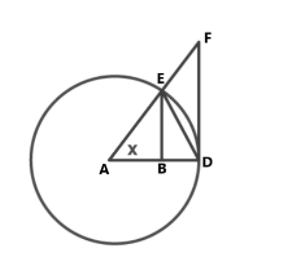
we see Δ ABE, Δ ADF, Δ ADB and area ADB.
Presently, AB = AD (isosceles traingle)
Region (ΔAED) < (area ADE) < Area (ΔADF)
1/2.AD.EB <( x/2π).π.AD2 < 1/2.AD.DF
Dropping the normal terms from all sides, we get
EB < x.AD < DF
From Δ ABE, sinA = EB/AB, so EB = AB sinx (point A= point X)
Additionally, tanA = DF/AD, so DF = ADtanX
Be that as it may, AB = AD and
tanA = sinA/CosA
along these lines, AD.sinA < x.AD < AD.sinA/cosA
= 1 < x/sinX < 1/cosX
Taking reciprocals we get,
cosx < sinx/x < 1
Thus demonstrated.
Utilizing the above theorem, we can undoubtedly demonstrate a few other mathematical characters, for example,
x0sinx/x =1
x0 (1 – cosx)/x =0
We need to remember a few focuses while assessing the limits. Suppose while assessing a capacity where xap(x)/q(x) exists to such an extent that p(x) = 0 and Q(x) = 0. Then, at that point, in such cases, we change p(x) and Q(x) in such ways that we get 2 capacities. This can be said as p(x) = p'(x).p”(x) to such an extent that p'(x) = 0.
Likewise we get q(x)=q'(x).q”(x) to such an extent that q'(x)=0. We then offset the normal terms and we get as far as possible as
xap(x)/q(x) = p'(a)/q'(a)
Meaning of Sandwich Theorem – we have three essential streams. We have the River Euler. We have the River Newton. Also, we have the river, Tiny. We don’t by and large have any idea where Tiny goes, yet we realize he begins on the slopes and he finishes in the ocean. We know a couple of things about the waterways in the Kingdom of Rimonn. We realize that Euler is generally north of the River Newton. We realize that Tiny is generally north of Newton, but south of Euler. So we realize that Tiny fundamentally is consistently among Newton and Euler, we simply don’t know precisely where he goes.
We additionally realize that Euler and Newton get together. They get extremely close in a town called Moe. So because Tiny is encircled by Newton and Euler all through the whole length of the waterway, we realize that Tiny additionally needs to get together in the town of Moe. Since we realize that Tiny doesn’t cross Euler or Newton, and since they get together at Moe, Tiny should likewise get together at Moe.
Conclusion
The finish of the classical style ham sandwich theorem for limited Borel sets might be strengthened, without extra speculations there generally exists a typical bisecting theorem that contacts every one of the sets, that is to say, that meets the conclusion of each set. In the discrete setting, where the sets are limited (and the actions are counting measures), there generally exists a bisecting hyperplane that contains no less than one point in every one of the sets. Rather than the division finish of the old-style ham sandwich theorem, this separation and intersection end doesn’t continue to unbounded arrangements of limited measure.
