Profile
Settings
Refer your friends
Sign out
A rigid body is one on which the distance between two locations remains constant whatever force is put to it or we can say a rigid body, on the other hand, is one that does not deform under the action of forces.
However, in real life, there would be some force that causes the body to deform.
A bridge, for example, does not sag under the weight of a single person, but it may sag under the weight of a vehicle or a fleet of ten trucks The distortion, however, is minor.
Rigid Body Dynamics
There are two types of motion that a Rigid Body undergoes that is
Translational Motion
A body is considered to be experiencing translational motion when it is shifted or moved from one location to another. It is the motion of a moving body in which all of its points move in the same line or direction. There is no change in an object’s orientation relative to a fixed point when it is undergoing translational motion.
So,Pure translational motion occurs when an object moves in such a way that all of its particles move in the same direction.
In this sort of motion, all locations of the body have the same magnitude and direction of velocities and accelerations at all times. The trajectories of all the points are the same. This means that when trajectories are stacked one on top of the other, they will coincide. In essence, the body’s orientation is fixed in relation to a single axis.
Some examples of translational motion are moving in a bus,sailing a boat, A plant being shaken by a person.
Rotational Motion
We examined motion in a circle at constant speed and, as a result, constant angular velocity in the section on uniform circular motion. Angular velocity, on the other hand, is not always constant—rotational motion might accelerate up, slow down, or reverse directions. When a spinning skater pulls in her arms, a youngster pushes a merry-go-round to make it spin, or a CD grinds to a halt when switched off, the angular velocity is not constant. Because the angular velocity changes in all of these circumstances, angular acceleration occurs. The angular acceleration increases when the change happens faster. The rate of change of angular velocity is known as angular acceleration. Angular acceleration is expressed as an equation.
α=Δω/Δt
Types of Translational Movement
Rectilinear motion
The body is in a straight line as it moves. Example. A ball flew off the edge of the cliff, A bullet from the pistol was discharged. Both uniform and non-uniform motions are possible.
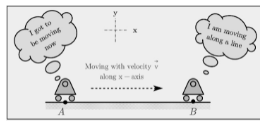
A cart is travelling from point A to point B in the diagram below. It is travelling at a velocity of v in a straight line (along the x-axis). This is the situation now.
It is in motion. As the cart moves in a straight path, the motion is rectilinear, and the motion is translatory, or translational, because all of the particles (or pieces) in the cart travel parallel to each other. Furthermore, the cart’s orientation remains unchanged.
Please keep in mind that we’re only considering the cart’s net linear velocity from point A to point B. We don’t take into account the motion its wheels make in order to get from point A to point B. The rolling motion of the cart’s wheels involves both translational and circular
Motion in a curved line
When the body moves in a curved path, this is the motion. It’s also two- and three-dimensional motion. As a result, pure translational motion does not have to be in a straight line all of the time. If an object goes in a curved path without changing its orientation, this situation is feasible.
Example. Motion of a projectile
Motion that is translatory (type curvilinear)
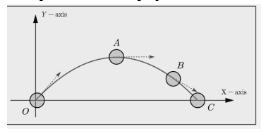
A parabolic path is followed by a ball.
The ball in question is thrown from point O and travels through points A and B to arrive at point C, as shown in the diagram. Projectile motion is the name for this type of movement. Curvilinear motion is the nature of projectile motion. To get from point O to point C, the ball is moving in a curved path rather than a straight line.
Conclusion
The number of various perceptions of rotation on the body that may be produced is zero. As a result, when the net force and net torque acting on the body is zero, we can deduce that the rigid body is in mechanical equilibrium. The directions must be taken with suitable sign conventions because the forces and torques are vector quantities.
