The energy that an object has as a consequence of its motion is known as kinetic energy.
We must apply force to an object if we want it to accelerate. Applying force requires effort. After the work is completed, energy is transferred to the item, which then moves at a new steady speed. Kinetic energy is the amount of energy transmitted and is determined by the mass and speed achieved.
Kinetic energy is a type of energy that may be exchanged between objects and converted into other forms of energy. A flying squirrel, for example, could crash with a motionless chipmunk. Some of the squirrel’s initial kinetic energy may have been transferred to the chipmunk or converted to another kind of energy after the collision.
Kinetic Energy
It is an object’s ability to perform work as a result of its motion. Wind, for example, has the kinetic energy to rotate the blades of a windmill and so produce electricity. The kinetic energy of an item is stated as, where K is the object’s kinetic energy in joules (J), m is the object’s mass in kilograms, and v is the object’s velocity:
Therefore it is represented as:
K = 1/2mv²
Expression for kinetic energy of an object
As we all Know that the energy of a body due to its motion is known as kinetic energy.
Derivation:
Let us consider we have an object of mass ‘m’ which is at rest on a plane. Let a force, F acts on the object and let us consider that the object moves from point A to point B and covers a displacement S.
Now the work done is given by:
W=F×S……..(1)
Work done = Force × Displacement
Now from the third law of Motion, we know that
V²-U²=2aS
S=(V²-U²)/ 2a………(2)
By Newton’s Second Law of Motion:
F=ma
Now, from the equation 1 and 2 we get
W=m×a×V²-U²/2a
As we assume that the object is at rest, Hence u=0
W=m×V²/2
Therefore, the Work done appears as kinetic energy of the body.
Hence,
Kinetic Energy=K.E=(1/2mv²)
Properties of Kinetic Energy
There are following properties of kinetic energy:
- Kinetic energy is related to the object’s velocity squared. This indicates that as an object’s velocity doubles, so does its kinetic energy.
- An automobile going at 60 miles per hour has four times the kinetic energy of a car travelling at 30 miles per hour, resulting in four times the potential for death and damage in the case of a collision.
- Kinetic energy must always have a positive or zero value. Regardless of whether velocity is positive or negative, velocity squared is always positive.
- Kinetic energy is a type of energy that is not a vector. A tennis ball thrown right with a velocity of 5 m/s has the same kinetic energy as a tennis ball thrown down with the same velocity.
Time period of a Simple Pendulum
A heavy point mass (called bob) is linked to one end of a completely inextensible, flexible, and weightless rope in an ideal simple pendulum. In actuality, we make it by threading a tiny cotton stitching thread through a metallic spherical bob.
A Simple Pendulum’s Length
The length of the simple pendulum is the distance between the point of suspension of the pendulum and it’s Center of Gravity (C.G.), which is the C.G. of the bob.
A Simple Pendulum’s Time Period
The time taken by the bob of a simple pendulum to complete one complete oscillation is called the time period. The letter T is used to signify it.
The pendulum begins a periodic motion when the bob is shifted to a particular angle, and the periodic motion is a simple harmonic motion with angular displacement of the bob for small values of the displacement angle.
F=mgsinθ
And
a=gsinθ
Let us Consider is small for the small oscillation
Therefore,
sinθ=θ=x/l
After Putting this value in a, we get
a=gθ
a=gx/l
Hence, the Angular Frequency is
ω=√g/l
And as we know that
T=2π/ω
Now after Substitution we get:
T=2π√l/g
So, based on the equation for the simple pendulum’s time period, we may deduce that the time period is independent of the pendulum’s mass and does not change with changes in the small amplitude of oscillation. It is entirely determined by the length of the string and the rate of acceleration. It has been commonly used to track a fixed interval of time because of this property.
Conclusion
In this article we are studying kinetic energy and derive an expression for it and also derive the time period of a simple pendulum. A simple pendulum is composed of a mass m suspended from a string with a length L and a pivot point P. When the pendulum is shifted to an initial angle and released, it will swing back and forth in a regular pattern and this is the working principle of a simple pendulum.
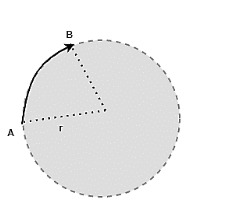
θ=AB/r= s/r
The rate of change of angle is defined as the angular velocity of the body. In the case of straight-line motion, it’s similar to velocity. The Greek letter omega (ω) is used to represent it.
ω=dθ/dt
Now we can use the value of θ in the above relation
ω=d/dt(s/r )
ω=ds/dt(1/r)
The velocity, v=ds/dt
Therefore,
ω=v/r
Uniform Circular motion
The human body has a natural tendency to travel in a straight path. There must be some force that keeps the bodies moving in a circular direction at a constant pace. The centripetal force is the name for such a force. Centrifugal force is the reaction of this force. This indicates that both forces are equal in magnitude and direction.
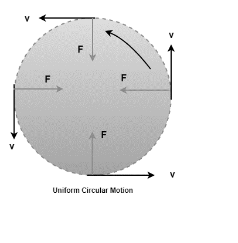
Centrifugal force can be given as,
F=mv²/r
We know that ω=v/r
F=m(ωr)²/r
F=mrω²
Centripetal force
Mechanical arrangements are difficult to meet the special demand of a continuously changing radial force. The condition specifies that the force must change direction in perfect sync with the particle. It’s a difficult task. This is especially true if we consider manipulating force by physically altering the mechanism that applies it.
Fortunately, natural and many cleverly devised arrangements generate scenarios in which the force on the body changes direction when the particle’s position changes – simply by moving. One such arrangement is the solar system, in which the planet’s gravitational attraction is always radial.
The force essential for circular motion is known as centripetal force. Centripetal force is the net component of external forces that meet this criterion. Centripetal force, in this sense, is not an independent force. Rather, we should consider this force as a component of the radial external forces acting on the body.
Direction of centripetal force and circular trajectory
Circular motion has a subtle point in terms of the direction of force imparted to the particle in circular motion. When a particle is at rest, it moves along the direction of the applied force rather than perpendicular to it. The situation is different in circular motion.
We impart centripetal force to a particle that is already travelling in the opposite direction of the force. As a result, the resulting motion from the interaction of motion with external force is tangential rather than radial.
The particle accelerates in the direction of centripetal force, i.e., towards the centre, according to Newton’s second law of motion. As a result, the particle has a downward displacement (Δy) with centripetal acceleration while also moving sideways (Δx) at a constant speed, because the component of centripetal force in the perpendicular direction is zero.
It may seem strange, but the particle is constantly descending towards the centre in the direction of centripetal force while also maintaining its linear distance from the centre due to persistent sideway motion.
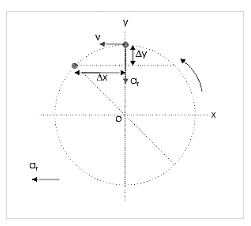
In the diagram, the particle goes towards the centre by Δy, while moving left by Δx at the same time. The vertical and horizontal displacements in the given period are such that the particle is always on the circle as a result of the resultant displacement.
∆x=v∆t
∆y=1/2ar∆t²
Conclusion
Circular motion can be both uniform and non-uniform. It is uniform circular motion if the tangential component of acceleration is absent, and it is non-uniform circular motion if the tangential component of acceleration is present. In the context of non-circular motion, the particle’s net acceleration is the sum of its radial and tangential accelerations.
Assume you’re in an inertial frame of reference and you’re watching a circularly moving particle. Because the particle has some acceleration, the net force on it must be non-zero, according to the second equation of motion. Take, for example, uniform circular motion. The particle’s speed is constant.
Centripetal force is defined as a force that is directed towards the centre. To keep the item in a uniform circular motion, this centripetal force is required. This is just the name given to this type of force, which can be caused by tension, friction, or other factors.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






