The Darcy–Weisbach equation is an empirical equation in fluid dynamics that connects the head loss, or pressure loss, caused by friction along a given length of pipe to the average fluid flow velocity for an incompressible fluid. Henry Darcy and Julius Weisbach are the names of the equation. There is currently no more accurate or generally applicable formula than the Darcy-Weisbach formula with the addition of the Moody diagram or Colebrook equation.
The Darcy friction factor is a dimensionless friction factor found in the Darcy–Weisbach equation. The Darcy–Weisbach friction factor is also known as the friction factor, resistance coefficient, or flow coefficient.
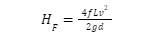
Where,
HF = head loss or pressure loss
F = coefficient of friction or friction factor
V = velocity of incompressible fluid
L = length of the pipe
D = diameter
G = acceleration due to gravity
Derivation of Darcy Weisbach equation

Step 1: terms and assumptions
Consider a horizontal pipe with a constant diameter d and an area A that allows an incompressible fluid to flow continuously.
Consider two parts of the pipe, S1 and S2, separated by a distance of L.
The pressure is P1 and the velocity is V1at all points of S1.
The pressure is P2 and the velocity is V2 at all points of S2.
Take a look at the fluid flow in the diagram (1) As a result, the pressure at S1 is larger than the pressure at S2, resulting in (P1>P2). This pressure differential causes the fluid to flow down the pipe.
There will be energy loss due to friction while fluid flows. Bernoulli’s principle can therefore be applied.
Bernoulli’s principle
According to Bernoulli’s principle, lowering the pressure or potential energy of a fluid increases the velocity/speed of the fluid flow, or in other words, “the sum of its potential energy, pressure, and velocity remains constant for incompressible fluid.”
Step 2: applying Bernoulli’s principle
We get the following results when we apply Bernoulli’s equation to sections S1 and S2:

As a result of rearranging equation (3) for the head loss, we get the following:
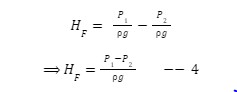
Step 3: Find frictional resistance
Friction provides resistance to the flow of fluid due to the combined action of wet surface and surface roughness. As a result, the speed of the process is slowed. The first person to notice the relationship between frictional resistance and surface roughness was Froude.
Froude’s formula accurately expresses frictional resistance.
Let’s call the frictional resistance per unit area(wet) per unit velocity f’.
Frictional resistance F = f’ × wet area × (velocity)²
=f‘=2πrL×v²
=f‘=πdL×v²
F=f‘=PL×v² –(5)
hered=2rdiameter, p=πd(perimeter)

- Fluid Frictional Force(F): Because it is a resistive force, it has a -ve direction.
As a result of resolving all forces in the horizontal direction, we get-


Application of Darcy Weisbach equation
Is used to calculate the loss of head due to friction in the pipeThe head loss and the volumetric flow Q within a pipe (that is, its productivity) per unit length S (the associated power consumption) are often the critical important parameters in a hydraulic engineering application. As a result, with a constant volumetric flow rate Q, head loss S reduces as the inverse fifth power of the pipe diameter, D. Doubling the diameter of a pipe of a specific schedule (for example, ANSI schedule 40) typically times the quantity of material required per unit length, and consequently the expense of installations. In the meantime, the head loss has been reduced by a factor of 32. (about a 97 percent reduction). Thus, for a small increase in capital cost, the energy consumed in moving a given volumetric flow of the fluid is drastically reduced.
History
This equation began as a variation of the Prony equation, which was invented by Henry Darcy of France and improved by Julius Weisbach of Saxony in 1845 into the form used today. Because data on the fluctuation of fD with velocity was inadequate at the time, the empirical Prony equation beat the Darcy–Weisbach equation in many circumstances. It was eventually replaced in many special-case circumstances by a number of empirical equations valid exclusively for specific flow regimes, such as the Hazen–Williams equation or the Manning equation, which were all much easier to calculate.
Advantages
The Darcy-Weisbach formula is ideal for calculating flow in pipes because of its precision and universal application. The following are the benefits of the equation:
- It’s founded on the fundamentals.
- It can be used with a variety of fluids, including oil, gas, brine, and sludge.
- In the laminar flow zone, it can be calculated analytically.
- It’s useful in the area where laminar flow meets fully formed turbulent flow.
- The diversity in friction factor is extensively established.
Conclusion
The Darcy Weisbach equation is empirical because it approximately links the loss head or loss pressure due to friction along a pipe length to the average fluid flow velocity for an incompressible fluid. Sir Henry Darcy and Julius Weisbach are the names of the equation.
The Darcy factor of friction is a dimensionless factor of friction found in the equation. The Darcy Weisbach factor of friction, often known as the resistance coefficient or the flow coefficient, is a measure of friction.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






