Profile
Settings
Refer your friends
Sign out
Introduction
The slope of a line is a measurement of the line’s steepness and direction. We can find the slope of lines in a coordinate plane and can assist forecast whether they are parallel, perpendicular, or none. Any two different points sitting on a line can be used to compute the slope. The slope of a line formula determines the proportion of “vertical change” to “horizontal change” between two points on a line.
Slope
The change in y coordinate with respect to the change in x coordinate of a line is known as its slope. The y coordinate’s net change is y, while the x coordinate’s net change is x. As a result, the y coordinate change in relation to the x coordinate change can be represented as,
m = Δy / Δx which is known as the slope of a line
And also tan θ = Δy/Δx
We can also say that tan θ to be the slope of the line.
Slope of a line
The ratio of the rise to the run, or the rise divided by the run, is the line’s slope. In the coordinate plane, it describes the steepness of a line. Finding the slope between two locations is comparable to calculating the slope of a line. In general, we require the values of any two separate coordinates on the line to compute the slope of a line.
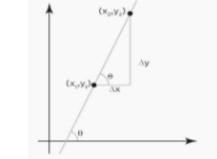
Slope between two points
Two points on a straight line can be used to compute a line’s slope. The slope of line formula can be applied using the coordinates of the two locations. P1 = (x1, y1) and P2 = (x2, y2) are the coordinates of those two points .
The slope is defined as “change in y coordinate with respect to change in x coordinate of that line,” as we described in the previous sections. So, when we plug the values of y and x into the slope equation, we get:
Δy = y2 – y1 , Δx = x2 – x1
As a result, we can calculate the following ratio using these values:
M = tanθ = (y2 – y1)/ (x2 – x1)
Where m denotes the slope and denotes the angle formed by the line with the positive x-axis.
Slope of a line formula
The slope of a line can be computed using the line’s equation. The general formula for a line’s slope is:
Y = mx + b
Where,
The slope is m, and the angle formed by the line with the positive x-axis is m = tanθ = Δy/Δx
The net change in the y-axis is Δy.
The net change in the x-axis is Δx.
Types of slope
Depending on the relationship between the two variables x and y, and thus the value of the gradient or slope of the line acquired, we can categorise the slope into different forms. There are four different sorts of slopes:
- Positive slope
- Negative slope
- Zero slope
- Undefined Slope
Positive slope
A positive slope means that the line rises as it moves from left to right in the coordinate plane, indicating that as x grows, so does y.
Slope is negative.
A negative slope means that the line falls as it moves from left to right in the coordinate plane, indicating that when x grows, y lowers.
Slope of 0
Because the rise is 0 for a line with zero slope, we can use the rise over run formula to determine the line’s slope.
Slope Undefined
The value of the run is zero for a line with an unknown slope. A vertical line’s slope is unspecified. Any slope that makes a 90⁰ angle with the x-axis will have an undefined tangent of 90⁰ value. As a result, the slope of such lines will be indeterminate.
Slope of horizontal line
A horizontal line is a straight line in a coordinate plane that is parallel to the x-axis and drawn from left to right or right to left. As a result, the horizontal line’s net change in y-coordinates is zero. A horizontal line’s slope can be expressed as,
m = Δy/Δx = zero is the slope of a horizontal line.
Vertical Line Slope
A vertical line is a straight line in a coordinate plane that is parallel to the y-axis and drawn from top to bottom or bottom to top. As a result, the net change in the vertical line’s x-coordinates is zero. A vertical line’s slope can be expressed as,
A vertical line’s slope, m = Δy/Δx is undefined.
Conclusion
We’ve seen lines drawn on the coordinate plane in geometry. The best approach to determine if the lines are parallel, perpendicular, or at any angle without using any geometrical tools is to measure the slope. The slope of a line, in general, indicates its steepness and direction. Finding the difference between the coordinates of two places (x1,y1) and (x2,y2) may simply compute the slope of a straight line between them. The letter ’m’ is commonly used to denote the slope.
