The inclination of parallel lines is the same. A house’s floor and ceiling, for example, are parallel to one other. The lines in the illustration below are also parallel.
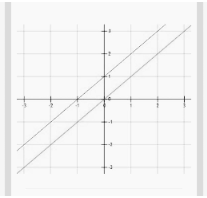
Two lines are mathematically parallel if and only if they have the same slope. Two such lines can never cross.
However, there are an endless number of parallel lines to each particular line. Because parallel lines might have distinct x and y intercepts, this is the case. There are infinitely many parallel lines because there are infinitely many possible y-intercepts.
Finding Parallel Line’s Slope
Finding the slope of a parallel line is rather straightforward if we grasp what parallel lines are and how to find slope in general.
There are two methods for determining the slope of a line parallel to a given line. Either we already know or we don’t know the slope of the provided line.
Finding for Parallel Lines When the Slope is Determined
The slope of the parallel line is exactly the same as the slope of the provided line.
You may be requested to find the equation of a certain parallel line in various instances. We can readily input the slope and intercept values into the slope-intercept equation if we know the y-intercept of this line.
We can also insert values into the point-slope equation if we know another point other than the y-intercept. The equation can then be transformed into slope-intercept form by solving for y.
Finding Parallel Lines Without Knowing the Slope
In some circumstances, we may be provided a line with a verbal description or a graphical representation that does not include a slope. If this is the case, we must first solve for the slope of the parallel line or lines before determining the slope of the parallel line or lines.
Remember that if we know two points, we can solve for the slope of a line. These two points are frequently included in verbal descriptions. “A line crosses between the points (1, 3) and (3, -4),” for example, we might know.
If we are given a graphical representation of a line, we may have to find two points.
The slope formula is the same in both cases:
m=(y1-y2)/(x1-x2).
After we’ve located the slope, we can proceed in the same manner as before.
Definition of a Perpendicular Line
Before going over the slope of a perpendicular line, it’s important to first define one.
If two lines meet at a straight angle, they are perpendicular.
The x and y axes, for example, are perpendicular to each other in the coordinate plane.
There are an unlimited number of lines parallel to any given line, just as there are an endless number of lines perpendicular to any given line. This is because perpendicular lines will meet at exactly one point, and in two-dimensional space, there is precisely one perpendicular line for each point on a given line. Because a line can have an unlimited number of points, it can also have an endless number of perpendicular lines.
Perpendicular Line’s Slope
The slopes of two perpendicular lines are the reciprocals of each other’s slopes.
Remember that n-1 is the reciprocal of n. We can also conceive of it in terms of 1/n.
The reciprocal of n is q/p if n is a fraction p/q. This is due to the fact that
1/p/q is equal to 1÷p/q=1/1×q/p=q/p.
The reciprocal with the opposite sign is the opposite reciprocal of a number. The slope of a perpendicular line is negative if the slope of a line is positive. If the slope of a line is negative, on the other hand, the slope of the perpendicular line is positive.
How to Determine a Perpendicular Line’s Slope
It is considerably easier to find the slope of a line perpendicular to a given line if we already know the slope of the provided line, much as it is with parallel lines. If not, we must first locate the slope. We divide the change in y-values for two points by the change in x-values for the same two points, as we always do.
When we know a line’s slope, m, we can predict that any line perpendicular to it will have a slope equal to the reciprocal of m. The slope will therefore be -m-1.
Finding a Perpendicular Line’s Equation
We frequently need to determine the equation of a line perpendicular to a given line that intersects it at a particular location. We start by determining the slope of the perpendicular line. The slope and intersection point data can then be entered into point-slope form. Finally, by solving for y, we may convert the point-slope form to slope-intercept form.
But what if we’re given another perpendicular line point and asked to find where it intersects the previous line?
The values of the slope and the specified point for the perpendicular line can be plugged into the point-slope equation as before. We then set the slope-intercept equation for the perpendicular line equal to the slope-intercept equation for the provided line once we obtain it.
This works because we want to find the value of x that produces the same value of y in either of the two equations.
We’ll arrive at the equation m1x+b1=m2x+b2.
Conclusion
Two lines are mathematically parallel if and only if they have the same slope. Two such lines can never cross.However, there are an endless number of parallel lines to each particular line. Because parallel lines might have distinct x and y intercepts, this is the case. There are infinitely many parallel lines because there are infinitely many possible y-intercepts.If two lines meet at a straight angle, they are perpendicular.The x and y axes, for example, are perpendicular to each other in the coordinate plane.The slope of a perpendicular line is negative if the slope of a line is positive. If the slope of a line is negative, on the other hand, the slope of the perpendicular line is positive.It is considerably easier to find the slope of a line perpendicular to a given line if we already know the slope of the provided line, much as it is with parallel lines. If not, we must first locate the slope. We divide the change in y-values for two points by the change in x-values for the same two points, as we always do.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






