Rotation

When we talk about rotation in mathematics, we are talking about a transformation that revolves around a figure around a fixed point known as the centre of rotation. In rotation, there is a fixed point at the centre of the circle, and everything else revolves around that point as it rotates. With another way of putting it, rotation can be defined as the motion of a rigid body around a fixed point. The item and the rotation of the object are both the same size and shape. So the figures can be rotated in any direction they want without losing their shape. In general, a rotation can occur in either a clockwise or counterclockwise direction. It is important to note that a clockwise rotation has a negative magnitude, whereas a counterclockwise rotation has a positive magnitude. For better or worse, a rotation is a turn of a shape, and it can be characterised by three parameters: its direction, its angle of rotation, and its centre of rotation, which is a point around which the shape revolves (see figure). Each point on the shape must maintain a constant distance from the centre of rotation in order to function properly.

Formula for Rotation

In both the clockwise and counterclockwise directions, rotation can be accomplished. The most common rotation angles are 90 degrees, 180 degrees, and 270 degrees. A clockwise rotation, on the other hand, denotes a negative magnitude, whereas a counterclockwise rotation implies a positive magnitude. Rotation in the coordinate plane is governed by a set of laws that must be followed. They are as follows:

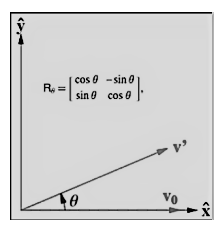
Rotation Matrix

It is possible to conduct a rotation in Euclidean space using a rotation matrix, which is defined as follows: In a two-dimensional cartesian coordinate plane system, the matrix R rotates the points in the XY-plane counterclockwise through an angle of with respect to the origin of the coordinate plane system. The matrix R can be represented in the following ways:

If we want to conduct the rotation operation on the plane using the rotation matrix R, the position of each point in the plane is represented by a column vector “v,” which contains the coordinate point for that point. The rotated vector can be obtained with the aid of the matrix multiplication Rv function.

Rotational Symmetry

Many geometric shapes, such as circles, squares, and rectangles, among others, exhibit rotational symmetry. All of the regular polygons exhibit rotational symmetry, including the irregular polygons. When an object is rotated around its axis, the object appears exactly as it did before the revolution took place. The object is said to have rotational symmetry if this is the case. There are a variety of methods for identifying rotational symmetry. For example, counting how many times the figure coincides with itself when rotated through 360 degrees is one of the simplest methods of determining the order of symmetry.

Rotation Images

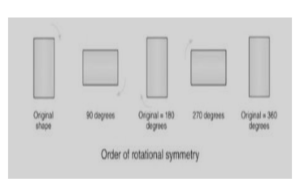
The sample above illustrates the rotation of a rectangle by 90 degrees on each iteration. As a result of its rotational symmetry of order 2, the rectangle has the following properties: when turned twice, we obtain the original shape at 180°; and again, when rotated twice more, we obtain the original shape at 360°. As a result, the rectangle has rotational symmetry in the second order.

Representing rotation using bivectors

When we represent rotation with bivectors, we may represent the rotation angle with a single scalar quantity, and rotations can be concatenated by adding and subtracting the angles from one another.

Increasing the number of dimensions involved in a rotation makes it more difficult to do. Projecting an object onto a two-dimensional plane and then rotating it through an angle can be used to depict any rotation. A bivector can be used to specify the plane (see the directed area box on the right of this page). A bivector is generated by multiplying two vectors of different lengths. The following table illustrates the dimension of the bivector produced by the multiplication of two vectors of different lengths. It just so happens that in three-dimensional vector space, bivectors have three dimensions as well, and as a result, three-dimensional rotations have three degrees of freedom.

When dealing with linear translations, for example, I could move an item up to three units (represented by [0,3,0]) and then move the object to the right four units (represented by [1,3,0]). (represented by [4,0,0]). This would result in a position of [4,3,0], which is simply the outcome of a basic vector addition operation. The order in which I perform these operations is not critical; for example, [0,3,0]+[4,0,0] = [4,0,0] + [0,3,0] is not critical. This does not result in the creation of a component in the z dimension in either situation. As a result, we cannot make these assumptions in the rotational case; we cannot find the result of applying subsequent rotations by simply adding vectors; and because the order in which the rotations are applied is critical, we must use different types of algebra, such as matrices and quaternions, to determine the effect of combining rotations.

Conclusion

A rotation is a circular motion in which a figure is rotated around a ‘centre of rotation.’ When you rotate about the origin, the point at which the rotation begins becomes the centre of rotation (0,0) The letter o stands for ‘degrees’. On the first graph, the original figure has been rotated 90 degrees around its axis of rotation.