Mode Deviation for Grouped and Ungrouped Data

One of the values of the measures of central tendency is the mode. This number gives us a general notion of which data set elements are most likely to occur. For instance, we are aware that a college offers 10 different course options to its students. The course with the greatest number of student registrations will now be used as the method of our provided data out of these number of students taking each course. Overall, the mode provides information on the item in the data set that occurs the most frequently.

Finding the mean or median won’t help you locate the course with the most students enrolled in it. So, under these circumstances, we frequently use Mode. 

We will go over how to determine the mode of both grouped and ungrouped data in this article.

What is Mode Deviation?

A value or number that appears most frequently in a dataset is referred to as the mode. We might occasionally need to identify the value that appears more frequently in the dataset. In these situations, we determine the mode for the given collection of data. 

Formula for Mode

The mode or modal value of a given collection of data is determined using the mode formula in statistics. It is characterized as the value that consistently appears in a particular set. 

How to Calculate the Mode Deviation for  Grouped and Ungrouped Data 

We are aware that a set of data’s mode refers to the value that appears the most frequently. The approach to finding the mode can now be modified based on the provided data (grouped or ungrouped). 

Mode deviation for grouped data

Use the methods listed below to determine the mode for grouped data.

• Find the class interval with the highest frequency as the first step. Modal class is another name for this
• Determine the class size. By deducting the upper limit from the lower limit, this is computed
• By Using the formula of mode , determine the mode

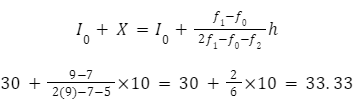
Where,

L is the modal class’s lower limit, 

h is the class interval’s size, 

f_m is the frequency of the modal class, 

f₁ is the frequency of the modal class’s predecessor class.

f₂ is the frequency of the modal class’s successor class.

Mode deviation for Ungrouped Data Mode

Ungrouped data refers to data that does not appear in groupings.

Simply arrange the data values either in ascending or descending order, then look for the repeated values and their frequency to determine the mode for ungrouped data. The modal value for the provided data is here defined as the observation having the highest frequency.

Examples of Mode Deviation

1. For the class interval and frequency listed in the table, determine the mode for the grouped data.

Solution:

Class interval	frequency
10-20	5
20-30	7.
30-40	9
40-50	5
50-60	4

Maximum class frequency is 9 so ƒ_m orƒ₁=9

Class interval corresponding = 30-40

Modal class lower limit (I) = 30

Size class interval (h) =10

The frequency of the class before the modal class (ƒ₀) = 7, and the frequency of the class after the modal class (ƒ₂) = 5

Using these numbers as replacements in the mode formula

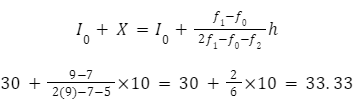
Answer: mode = 33.33

2. From the following table, determine the mode of the ungrouped data.

Solution:

Color of car	Red	Blue	Silver	Black	Yellow
No. of car solid	10	12	20	15	11

We will look at the class with the highest frequency to determine the mode of the ungrouped data. The most common class of vehicle in this instance is one that is “Silver” in color. Therefore, 20 is the mode.

 Answer: mode  =20

Conclusion

In this article we learned that the value(s) that appear in a dataset the most frequently are represented by the mode. When the mean and median cannot be employed, the mode informs us of the most prevalent value in categorical data. The mode provides us with a sense of where the “center” of a dataset is, although it is less reliable than the mean or median.