Distance Formula

The distance formula is a method for calculating the distance between two places. These points can be of any size and in any dimension. You might want to find the distance between two points on a line (1d), two points in a plane (2d), or two locations in space (2d), for example (3d).

Many forms of  Distance formulas – 

• The distance between two points in a two-dimensional plane.

• In a three-dimensional plane, the distance between two points.

• The distance between a point and a line in two dimensions.

• The distance between two parallel lines in two dimensions

• The distance between a point and a line in three dimensions.

Pythagorean Theorem

Pythagorean theorem describes how the three sides of a right-angled triangle are related. The square of the hypotenuse is equal to the sum of the squares of the other two sides of a triangle, according to Pythagoras’ theorem. 

Hypotenuse2 = Perpendicular2 + Base2 

         c2 = a2 + b2  

Consider the following triangle:

The perpendicular is denoted by “a.”

The base is “b.”

The letter “c” symbolizes the hypotenuse.

Derivation of distance Formula 

Distances between points in rectangular coordinates are calculated using the Pythagorean Theorem.

The distance between the points (a,b) and (c,d) is given by Square root of √(a − c)2 + (b − d)2. The distance between the points in three-dimensional space is called the distance between the points. (a, b, c) and (d, e, f) is Square root of √(a − d)2 + (b − e)2 + (c − f)2.

Distance formula derivation

According to Pythagoras’ theorem,

The formula for calculating the distance between two points is known as the distance between two points formula.

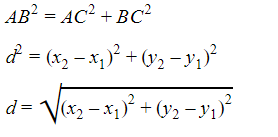
Applications of Distance Formula

The distance formula has a wide range of applications in mathematics.

• The distance formula can be used to compute the distance between any two points

• The arg-and plane is used to represent complex numbers, and the formula for finding their magnitude has been derived from the distance formula

The formula can be used to calculate the distance between two points in three-dimensional and n-dimensional planes.

• To find the magnitude of a vector, use the distance formula to construct the magnitude formula

• The distance between two points in a sea can be calculated using the distance formula and the geographic coordinates of the two points

Conclusion

A numerical representation of the distance between two objects or points is called distance. Distance can refer to a physical length or an approximation based on other physics or common usage factors. The pilot of a plane uses the distance formula to calculate the distance between their plane and the other plane. They determine the plane’s coordinates and then compute the distance using the distance formula.