Profile
Settings
Refer your friends
Sign out
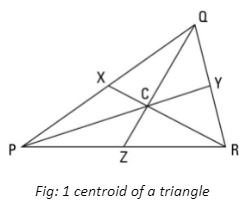
The centroid’s coordinates are just the average of the vertices’ coordinates. To obtain the orthocenter’s x coordinate, add the three vertex x coordinates together and divide by three. Carry on with the y coordinate. The triangle’s centroid is the point where all of the mass of a triangular plate appears to act. The names “center of gravity,” “center of mass,” and “barycenter” all refer to the same entity. The centroid is the point where the medians of the triangle intersect, which is an interesting fact. Understanding the centroid of a triangle is important. We’ll go over the definition of centroid, the formula, the attributes, and a few sample problems. A triangle is a three-sided shape with three internal angles.
Centroid of a triangle
The centroid of a triangle is the place where the triangle’s medians meet. Let’s look at the medians of a triangle before we go into the point of concurrency. The line segments drawn from the vertex to the mid-point on the opposite side of the vertex are known as medians. A triangle’s middle divides the triangle into two smaller triangles with equal areas. The centroid of a triangle is the place where the medians of the triangle intersect.
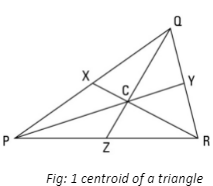
By calculating the medians, the above picture represents the centroid of a triangle. The line segment from the vertex of the triangle to the midpoint of the opposite side of the triangle is used to draw the median. In a 2:1 ratio, the centroid splits the median.
Properties of Centroid of a triangle
Below properties of a triangle’s centroid aid in identifying it from all other points of concurrence.
- The geometrical center of a triangle is sometimes called the centroid.
- The triangle’s centroid is the point in which the triangle’s three medians intersect.
- A triangle’s centroid is always situated within the triangle.
- In a triangle, the four different points of concurrency based on different criteria are the centroid, circumcentre, in Center, and orthocenter. The centroid is the most generally recognized point of concurrency among these.
- In the ratio, the centroid divides the median. 2:1
Triangle’s Centroid Formula
This formula is used to calculate the coordinates of a triangle’s centroid when the triangle’s vertices are known.
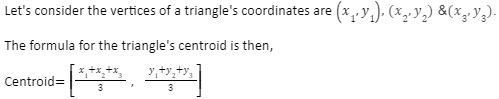
Conclusion
The coordinates of the centroid are just the average of the coordinates of the vertices. Add the three vertex x coordinates together and divide by three to get the orthocenter’s x coordinate. Continue working with the y coordinate. The object’s centroid is its center point. The centroid of a triangle is the point where the triangle’s three medians meet. It’s also known as the point where the three medians meet. The median is a line that runs from the midpoint of one side to the corresponding vertex of a triangle. The triangle’s centroid divides the median from the median in a 2:1 ratio. Averaging the x- and y-coordinate points of all the triangle’s vertices can be used to calculate it. The triangle’s centroid is the point where the triangle’s medians meet. Before we get into the point of concurrency, let’s look at the medians of a triangle. The medians are the line segments drawn from the vertex to the mid-point on the opposite side of the vertex. The center of a triangle divides it into two smaller triangles with equal areas. The intersection of the triangle’s medians is where the triangle’s centroid is located.
