Every place on the planet has coordinates that allow us to quickly locate it on a world map. Our planet’s coordinate system is made up of imaginary lines known as latitudes and longitudes. The zero degrees of ‘Greenwich Longitude’ and zero degrees of ‘Equator Latitude’ are the beginning lines of this coordinate system.’ In the same way that the horizontal x-axis and the vertical y-axis are used to locate a point in a plane or on a piece of paper, we have the coordinate axes with the horizontal x-axis and the vertical y-axis.
The study of geometric figures using coordinate axes is known as coordinate geometry. Straight lines, curves, circles, ellipses, hyperbolas, and polygons can all be readily drawn and scaled in the coordinate axes. Furthermore, using the coordinate system to work algebraically and examine the attributes of geometric figures is referred to as coordinate geometry.
Coordinates Concept
- The origin is defined as the place where the x and y axis cross. Both x and y are zero at this point.
- The positive numbers on the right-hand side of the x-axis are greater than the negative values on the left-hand side.
- Similarly, on the y-axis, positive values are found above the origin, while negative values are found below the origin.
- A collection of two integers is used to establish the location of a point on the plane. So, first, write about where it is on the x-axis, then write about where it is on the y-axis. The two will
work together to select a single and distinct place on the plane.
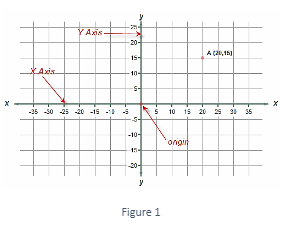
The values to the right of the x-axis are positive, while those to the left are negative.
On the y-axis, positive numbers are above the origin, while negative values are below.
Coordinates of a Point
A coordinate is a numerical value that aids in the location of a point in space. The coordinates of a point in a two-dimensional space are (x, y). Let’s have a look at these two crucial terms.
Abscissa: The x value in the point (x,y) as well as the distance from the origin along the x-axis are known as the abscissa.
Ordinate: It is the perpendicular distance of the point from the x-axis, which is parallel to the y-axis, and it is the y value in the point (x, y).
The coordinates of a point can be used to perform a range of tasks, including calculating distances. the slope of a line, determining the midpoint, and computing the equation of a line.
Coordinate geometry ratio formula (Section formula)
The section formula is useful for determining the coordinates of a point on a line segment that connects two points.x1,y1,(x2,y2) in the m:n ratio The point that divides the provided two points is located on the line that connects them and can be found either between the two locations or outside the line segment between them.
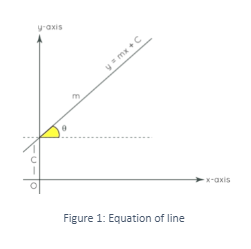
Find Equation of a Line in Coordinate Geometry
With the use of a basic linear equation, this line equation represents all of the points on the line. ax + by + c= 0 is the conventional form of a line equation. There are several methods for determining a line’s equation. The slope-intercept form of the equation of a line (y = mx + c) is another essential form of the equation of a line. The slope of the line is m, and the y-intercept of the line is c.
Applications of Coordinate Geometry
The following are a few examples of coordinate geometry applications.
- To find the location of cursors on computers, mobile phones, and other devices.
- In navigational maps (GPS).
- To locate geographical areas.
- It is used in a variety of mathematical topics, including algebra, calculus, functions, and complex numbers.
Conclusion
We studied at the definition of coordinate geometry in this article. The definitions of coordinates, axis, origin, and coordinate plane, as well as, have all been learnt. Coordinate geometry has a wide range of applications in mathematics. Many applications of coordinate geometry may be found in math topics such as vectors, three-dimensional geometry, equations, calculus, complex numbers, and functions. All of these issues necessitate the presentation of data graphically in a two/three-dimensional coordinate plane. Coordinate geometry is required to provide a link between algebra and geometry through the use of line and curve graphs. It is an important part of mathematics that helps us locate points on a plane. It also has numerous applications in trigonometry, calculus, dimensional geometry, and other sciences.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






