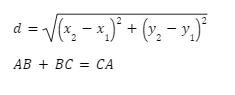Collinear Points

Mathematicians are highly precise with their words. Collinear points are points that are all in the same line in Euclidean geometry, whether they are close together, far away, or form a ray, line segment, or line. Collinear comes from the Latin terms ‘col’ and ‘linear,’ where ‘col’ means together and ‘linear’ means in the same line. Collinearity refers to the property of two points being parallel. Only 3 or more points that are in the same straight line are collinear. There is only one line that can pass through three different collinear locations.

The collinear points are P, Q, and R in the  below figure.

Figure 1: -Collinear Points

Collinear points properties

• The origin of two opposed rays can be viewed as a location on a line that lies between two other points on the same line.

• Lengths of segments If A, B, and C, are points on the same line, and B lies between A and C, then AB + BC = AC, according to the Segment Addition Postulate.

• Because collinear points are on the same line, the slope between them must be the same.

• Any convex polygon in the plane has just two vertices that are collinear.

Formula for Collinear Points

To determine whether three points are collinear, use the collinear point’s formula. There are several methods for determining whether or not three points are collinear. The Slope Formula, the Area of Triangle Formula, and the Distance Formula are the three most used formulas for determining whether or not points are collinear. Let’s go over each of these formulas one by one.

Slope formula

The slope of the lines created by the three points in question The three points are collinear if the three slopes are equal.

If we have three points x,y., the points will only be collinear if the slope of line xy equals the slope of line yz = the slope of line xz. The slope formula is used to determine the slope of a line connecting two locations.

The line joining points slope Px1.y1 & Q(x₂,y₂)

m= y₂-y1 / x₂-x₁

Area of Triangle Formula

This indicates that no triangle can be formed if any three points are collinear. As a result, we check the triangle’s points by plugging them into the triangle’s area formula.

Because the triangle created by three collinear points is only a line connecting the three locations, it has no area. The formula for calculating the area of a triangle, which is used to check for point collinearity, is:

area Triangle with the given points A(x1,y1) , B(x2,y2) & c(x3,y3)

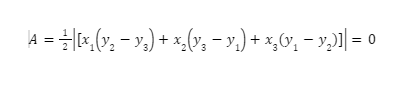
Distance formula

We find the distance between the first and second points, then the distance between the second and third points, using the distance formula. Following that, we check to see if the sum of these two distances equals the distance between the first and third points. Only if the three points are collinear will this be achievable. The distance formula is used to compute the distance between two places whose coordinates are known.

The distance of two points  A(x1,y1)and B(x2,y2)

So, if we have three collinear points in the order A, B, and C, AB + BC = CA, these points are collinear.

Conclusion

In this article we learn that the points that are collinear are those that are on the same straight line or on a single line. In Euclidean geometry, two or more points on a line that are close to or far from each other are said to be collinear. Ans Collinearity is the correlation between predictor variables (or independent variables) in a regression model that expresses a linear connection. When predictor variables in a regression model are correlated, they are unable to predict the value of the dependent variable on their own.