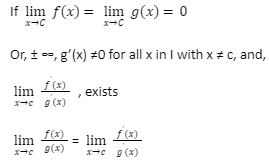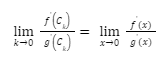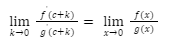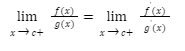Cauchy’s Mean Value Theorem and L Hospital’s Theorem

The Mean Value Theorem of Cauchy is a generalisation of Lagrange’s Mean Value Theorem. Cauchy’s mean value theorem is just a generalisation of the well-known mathematical result of the traditional mean value theorem. The Extended Mean Value Theorem, sometimes known as the Second Mean Value Theorem, is a well-known theorem. This is how it’s defined: There is at least one point on this interval where x = c, which is indicated by the symbol c, if a function (x) is continuous in the close interval [a, b] where (x b) and differentiable in the open interval [a, b] where (x b).

=f’ (c) f(b) – f (a) (b-a)

The link between derivatives of 2 functions as well as the changes in these functions over time is used to define a limited interval.

Consider the functions f(x) and g(x), which are continuous on the interval [a, b], differentiable on interval (a, b), and just not equal to 0 for all x. (a, b). Then in the interval f(b)-f(a) f’, there is a point x = c.

f(b) – f(a) / g(b) – g(a) = f’(c)/g’(c)

The denominator in the left side of the Cauchy formula is not zero because g(b)-g(a) is not equal to zero. Rolle’s theorem claims that if g(b) equals g(a), there exists a point d? (a, b) where g'(d) equals zero. Does the premise that g'(x) = 0 for all x contradict itself as a result? (a, b).

We’ll now make use of the auxiliary function.

By putting g (x) = x into Cauchy’s mean value theorem, the Lagrange formula is derived, which has the geometric interpretation that has been supplied. Consider how the parametric equations result in a curve. X = f (t) and Y = g (t), where t is the time and the parameter t is in the range [a,b].

The point of the curve in the above picture moves further from A (f) as the value of the parameter t is changed (a). A transformation is g(a) to B (f(b), g (b)).

What is the rule of L’Hospital?

The most significant rule in Calculus is L’ Hospital’s Rule (L’Hôpital’s rule). The derivatives are used in this rule to evaluate the limits that involve indeterminate forms. In this article, we’ll go over the formula & proof for L’Hospital’s rule, as well as some examples.

L’Hospital’s rule is a way for evaluating indeterminate forms like 0/0 or /. L’Hospital’s rule is used in calculus to determine the limits of indeterminate forms for derivatives. The L Hospital Rule can be used several times. You can apply the same rule indefinitely, and it will hold any indefinite form after each application. You can’t use L’Hospital’s Rule if the problem isn’t one of the indeterminate forms.

The Formula for L’Hospital’s Rule

The rule at L’Hospital is that

Note: If the supplied criteria are met, the limit of the quotient of function is identical to the limit of the quotient of their derivatives.

The evidence of L’Hospital’s Rule:

The L’Hospital’s rule can be established using the Extended Mean Value Theorem or Cauchy’s Mean Value Theorem.

If f & g are two continuous functions just on interval [a, b] that diverge on the interval (a, b), then f'(c)/g'(c) = [f(b)-f(a)]/[g(b)-g(a)] such that c is a member of (a, b).

Assume that the two functions f & g are defined just on interval (c, b) with f(x)0 and g(x)0, respectively, as xc+.

However, we have the fact that f'(c) / g'(c) tends to finite limits. The functions f & g are differentiable, as well as f'(x) and g'(x) exist on the set [c, c+k], and f’ and g’ are continuous on the interval [c, c+k] if f(c)= g(c) = 0 and g'(c) 0 are met, on the [c, c+k] interval.

By Cauchy Mean Value Theorem states that there exists ck∈ (c, c+k), such that

f’(ck)/g’(ck) = [f(c+k)-f(c)] /[g(c+k)-g(c)] = f(c+k)/g(c+k)

Now, k→0+,

While,

So, we have 

Mean Value Theorem:

Suppose that f is a function that satisfies:

f is continuous on the closed interval 

[a, b].

f is differentiable on the open interval (a, b).

Then there is a point c ϵ (a, b) or a < c < b, such that

F’(c) = {f(b) – f(a)} / b-a

The Mean Value Theorem asserts that a continuous, differentiable function will reach the speed (slope) equal to its average speed throughout an interval at some point between two points in the interval. This phenomenon will be depicted in an image that will be exhibited later.

The Mean Value Theorem asserts that if the average velocity (speed) of a continuous, differentiable function during a given period is zero, the function will have slope equal to the average speed of zero at some point in the interval. 

This is followed by a statement of Rolle’s Theorem, which demonstrates how it is a specific instance of the Mean Value Theorem, namely, when the function has a velocity of zero so over interval.

Conclusion:

Cauchy’s mean value theorem is indeed a generalisation of the well-known mathematical result of the traditional mean value theorem. The Extended Mean Value Theorem, sometimes known as the Second Mean Value Theorem, is a well-known theorem. 

This is how it’s defined: There is at least one point on this interval where x = c if a function (x) is continuous in the near interval [a, b] where (x b) and differentiable in the open interval [a, b] where (x b). L’Hospital’s rule is a general method for assessing indeterminate forms like 0/0 or / that can be used in any context.

 In calculus, L’Hospital’s rule is used to calculate the limits of indeterminate forms for a function’s derivatives. In a single case, the L-Hospital rule can be used several times. You can keep using this rule as long as it keeps any undefined form after the first time you used it.