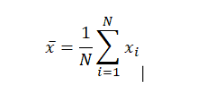Calculating Mean & Median

Introduction 

The “mean” is essentially an “average” in which all of the numbers are added together and then divided by the number of digits. The “median” of a number series is the “middle” value, while the “mode” is the value that appears frequently. Out of these three measures, the mode formula in statistics opens up several ranges and elements for the student’s consideration. Let’s get to know more about how to calculate mean and median.

Calculating Mean and Median

The mean is the first theory to grasp from the mean, median, and mode calculator. As previously stated, it is the ratio of the total of all values to the number of items. Simple arithmetic mean and weighted arithmetic mean are the two forms of Mean. 

Mean Formula 

Mean is commonly represented as x, pronounced “x bar,” and the bar notation is a popular signal of some form of the mean even when the variable is not x. Instead of utilising the variable x, the Greek symbol mu, or, is used in the case of the population mean. In statistics, the sample mean is sometimes displayed with a capital X, which is confusing.

The mean in this context refers to a value in the middle of a discrete set of numbers, meaning the sum of all values in the data set divided by the total number of values. With minor differences in the variables employed, the equation for calculating the arithmetic mean is nearly identical to that for computing the statistical notions of population and sample mean:

The median is a value that divides a data sample, population, or probability distribution into two halves in statistics. Finding the median entails locating a value in a data sample physically located in the middle of the other numbers. 

It’s worth noting that the order of the data samples matters when computing the median of a finite list of numbers. The values are usually listed in ascending order, but there’s no reason why listing them in descending order would produce different results. The median is simply the number in the center of the list of all values when the total number of values in a data sample is odd.

For instance, in the data 

2,10,21,23,23,38,38

Following the ascending sequence of the data and determining that there is an odd number of variables, it is evident that 23 is the median in this situation. If the data set were to be supplemented with another value

Because there are an even number of values, the median will be the average of the two middle numbers, which in this case are 23 and 23, with a mean of 23. It’s worth noting that the inclusion of an outlier (a number that falls outside the expected range of values), the value 1,027,892, does not influence the data set in this case. If the mean for this data set is computed, the result is 128,505.875. This value does not represent the seven other values in the data set. 

The median is the mean of the two middle values when the data sample has an even number of values. While this may seem perplexing, keep in mind that while the median may involve the computation of a mean, it will only involve the two middle values in this case, whereas a mean will include all of the values in the data sample.

While both and other statistical values should be calculated when summarising data, if there are particularly wide fluctuations between values, the median can provide a better indication of a typical value in a given data collection.

Central Tendency

The terms “mean,” “median,” and “mode” all refer to measures of central tendency. The mean, median, and mode calculator denote a data synopsis that depicts the dataset’s center point or quintessential value. These measures, often known as the central location of distribution, define where the majority of values in a distribution fall. 

Depending on the data, the best metrics of central tendency can be chosen. A “measure of central tendency” is a framework for evaluating a location parameter or a statistic for evaluating a location parameter.

Range

In statistics, the range of a data set is the difference between the greatest and lowest values. While the range has many meanings in different fields of statistics and mathematics, this is the most basic definition that the calculator uses. Using the example:  

2,10,21,23,23,38,38

38 – 2 = 36

In this case, the range is 36. Be it big or small numbers. It can considerably impact range. Continuing with the previous example,

2,10,21,23,23,38,38,1027892

In this scenario, the range would be 1,027,890, versus 36 in the prior case. As a result, it’s critical to examine data sets to account for outliers thoroughly. 

The basic arithmetic mean considers all data values equal and assigns equal weight to each one. Weighted arithmetic mean, on the other hand, assigns weights or emphasis to the values. 

Conclusion

Compared to the mean, the main benefit of utilizing the median is to describe statistical data. While both statistical values should be calculated when summarising data, when there are particularly wide fluctuations between values, the median can provide a better indication of a typical value in a given data collection. There are plenty of study materials on calculating the mean and median online.