The set of lines that intersect at a common point is known as concurrent lines. To qualify as concurrent lines, three or more lines must meet at a single place. Only lines can be concurrent; rays and line segments cannot be concurrent since they do not always meet at the same spot. A point can have more than two lines passing through it. The diameters of a circle are congruent at the circle’s center, for example. The line segments connecting the midpoints of opposite sides, as well as the diagonals, are contemporaneous in quadrilaterals.
Definition of Concurrent lines
“Concurrent lines are three or more lines that pass through a single point on a Cartesian plane. The point of concurrency is defined as the intersection of two concurrent lines.”
Concurrent lines properties
-
In 2-D geometry, concurrent lines are lines that cross each other exactly at one point.
-
Concurrent means that something is happening at the same time or in the same place.
-
The connecting lines are always at the same place.
-
Concurrent lines are non-parallel lines that stretch in both directions forever.
Figure 1: Concurrent lines
The “point of concurrency” is designated by the letter P. This idea may be found in the triangle’s many centers.
Concurrent Lines in a triangle
A triangle is a two-dimensional shape with three sides and three angles that has three sides and three angles. When some specific sorts of line segments are drawn inside triangles, concurrent lines can be visible. In a triangle, we can find four different places of concurrency.
Incenter: The incenter of a triangle is the place where three angular bisectors intersect inside a triangle.
Circumcenter: The circumcenter of a triangle is the point where three perpendicular bisectors intersect inside a triangle.
Centroid: The centroid of a triangle is the place where the three medians of a triangle coincide.
Orthocenter: The orthocenter of a triangle is the location where three altitudes of a triangle intersect.
Concurrent Lines Formula and Conditions for 3 Concurrent Lines
If three straight lines pass through a location and meet at that point, they are said to be concurrent.
As a result, if three lines are parallel, the intersection point of two lines is on the third line.
Let’s see what the equations of the three parallel straight lines are.
a1x+b1y+c1=0 …… (i)
a2x+b2y+c2=0 …… (ii)
a3x+b3y+c3=0 …… (iii)
As a result, the criterion for three lines concurrently is:
Example of Concurrent lines
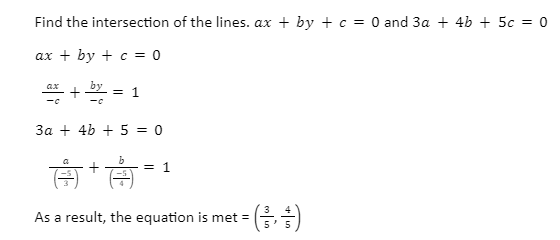
Conclusion
In this article, we studied concurrent lines in geometry, as well as concurrent lines in the triangle formed by the incenter, circumcenter, centroid, and orthocenter of a triangle. Solved examples relating to concurrent lines are also discussed. In 2-d geometry, concurrent strains are lines that overlap each other precisely at one factor. This indicates that the concurrent event is occurring at the same time or at the same location. Because these strains expand endlessly in both directions, they will meet at some point in the plane. As a result, we can state that all non-intersecting lines are parallel to one another. Concurrent lines are non-parallel lines that stretch in both directions forever. They cross in the plane at a place where they intersect. As a result, we can conclude that all parallel lines are not concurrent.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






