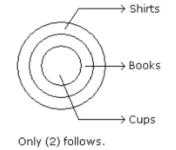
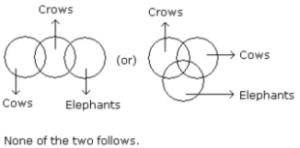
The syllogism is an essential component of all aptitude questions. It can be classified as logical reasoning. Due to their perplexing character, syllogisms have risen to prominence in aptitude tests over time.
The topic of syllogism is quite popular in government exams, and questions about it are almost always asked, as witnessed in recent years. As a result, a thorough comprehension of the concept is critical.
Syllogism Questions and Answers
Statement 1. actors also perform as singers. All of the performers are also dancers.
Conclusions:
- actors also perform as dancers.
- No actor is a singer.
A. There is just one conclusion.
B. There is only one (2) conclusion.
C. Either (1) or (2) comes next.
D.Neither (1) nor (2) are true.
E. Both (1) and (2) are true.
Answer. Option A.
Statement 2. The harmoniums are all musical instruments. Flute is the only instrument used.
Conclusions:
- The flutes are all musical instruments.
- Flute harmoniums are used throughout.
A. There is just one conclusion.
B. There is only one (2) conclusion.
C. Either (1) or (2) comes next.
D. Neither (1) nor (2) are true.
E. Both (1) and (2) are true.
Answer. Option B.
Statement 3. Yellow mangoes exist. Mangoes are among the tixo.
Conclusions:
- Green mangoes exist.
- The colour Tixo is yellow.
A. There is just one conclusion.
B. There is only one (2) conclusion.
C. Either (1) or (2) comes next.
D. Neither (1) nor (2) are true.
E. Both (1) and (2) are true.
Answer. Option D.
Statement 4. Parrot-like ants exist. The apples are all the parrots.
Conclusions:
- Every apple is a parrot.
- Some ants are similar to apples.
A. There is just one conclusion.
B. There is only one (2) conclusion.
C. Either (1) or (2) comes next.
D. Neither (1) nor (2) are true.
E. Both (1) and (2) are true.
Answer. Option B.
Statement 5. Some papers function as pens. All of the pencils are actually pens.
Conclusions:
- Pencils are some pens.
- Some pens are made of paper.
A. There is just one conclusion.
B. There is only one (2) conclusion.
C. Either (1) or (2) comes next.
D. Neither (1) nor (2) are true.
E. Both (1) and (2) are true.
Answer. Option E.
Syllogism Tricks
Candidates can use the syllogism tactics and strategies listed below to assist them easily solve syllogism questions:
- Always keep an eye out for words like ’some, a few, all, at least,’ and so on. These words serve as the foundation for answering syllogism questions.
- The most effective syllogism trick is to answer problems using Venn diagrams. This will help to clarify and simplify the explanation.
- When answering syllogism problems, never make assumptions.The data specified in the question is the sole data that must be followed when answering the question. When answering questions, no further assumptions must be made.
Solve the examples in this article using the syllogism approach mentioned earlier. These syllogism methods will come in handy when it comes to answering queries.
Tips for answering questions on syllogism:
- Carefully read the question.
- Begin creating a Venn diagram.
- While drawing, follow the question’s sequence.
- Examine the Venn diagram’s conclusion.
- At the end, look for additional possibilities.
Types of Syllogism Questions
All A are B
This statement implies that A is contained in B, but not necessarily the other way around. This indicates that A is a subset of B, but B is not always a subset of A. This is how the Venn diagram looks
In this picture, circle A is visible inside circle B, indicating that B contains all of A, i.e. all of A is B.
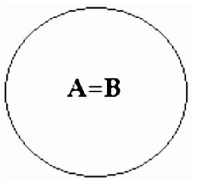
A = B
The conclusion in this example is similar to the previous type, namely, “All A are B.” Not only are “All A are B,” but “All B are A” as well. This signifies that A is a subset of B, and vice versa. The Venn diagram is as follows
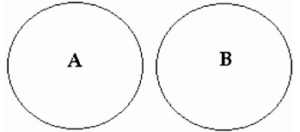
A is contained within B, and B is contained within A. As a result, A contains all of B, and B also contains all of A.
No A are B
It is self-evident that B does not include any of A, and hence A does not exist in B. A and B are therefore distinct sets. This case’s Venn diagram is as follows:
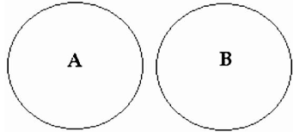
No part of A is contained within B, and no part of B is contained within A. As a result, neither A nor B contain any part of the other.
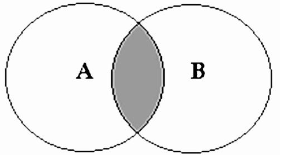
Some A are B
This is the case when some of A is in B, indicating that A and B intersect, and so some B is A. The Venn diagram looks like this
The shaded section shows that some of A is present in B, whereas the unshaded portion is ambiguous and does not indicate whether or not A is contained in B.
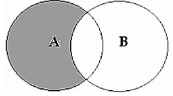
Some A are not B
This signifies that some of A is definitely not included in B, while the rest of A is unsure whether or not it is included in B. The Venn diagram is as follows
In this case, some of A is undoubtedly not included in B, whereas the shaded region is uncertainly included in B.
Applications
To familiarise the reader with the fundamental issue of our study, we shall enumerate the valid moods of the syllogism and offer some generalizations and remarks in this chapter. Validation will be covered in a separate chapter following that. Please keep in mind that we’re only talking about one form of proposition here: the actual, classificatory, categorical. Of course, other forms of propositions will require treatment at some point.
Classical logic, the showcase of science, which we owe to Aristotle and subsequent masters, is our primary interest here. There are a few minor related subjects that will be discussed as the project progresses.
Conclusion
The word “syllogism” comes from a Greek word coined as “syllogismos,” which simply translates as “conclusion, inference.” Syllogisms are logical arguments that employ logic and reasoning to conclude. Aristotle is known for making the most significant contribution to the field of syllogisms.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out