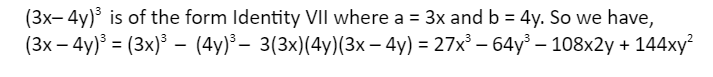Algebraic Identities

Algebra is one of the most important parts of Elementary Mathematics. It is introduced to students in the lower years of secondary education and continues through senior secondary and into higher education. Algebraic Identity is a broad topic with applications in almost every aspect of a student’s life. An algebraic identity is a formula that holds true no matter what value is applied to the variables in the equation. It signifies that the equation’s left-hand side (LHS) is always equal to the right-hand side RHS).

Definition of Algebraic identities:

Algebraic identities are equations that hold true for all possible values of variables. Numbers, variables (unknown values), and mathematical operators make up algebraic identities and expressions (addition, subtraction, multiplication, division, etc.)  Algebraic identities are utilised in a variety of mathematical fields, including algebra, geometry, and trigonometry. These are mostly used to find the factors of a polynomial. A deeper understanding of algebraic identities helps to improve the efficiency with which problem sums are solved. The factorisation of polynomials is among the most important applications of algebraic identities.

Everything About Algebraic Identities:

An identifier is an equation that holds true for all values of the variables in it. For all variable values, an algebraic identifier is an equation in which the value of the left-hand side of the equation equals the value of the right-hand side of the equation. In different disciplines of mathematics, we have several standard identifiers that we might use. The Binomial assertion yields all standard Identities. An algebraic identifier is an algebraic equation that refers to all of the values of a variable in it. It is also employed in the factoring of polynomials. As a result, algebraic identifiers are utilised to calculate algebraic expressions and solve various polynomials. In your younger classes, you must have learned about Algebraic Identities. You will review those ideas and improve your learning in this lesson.

How to verify algebraic identity?

The method of substitution is used to check that the algebraic identities are true. Substitute values for the variables and conduct the arithmetic operation with this method. The activity technique is another way to check the algebraic identity. You’ll need a basic understanding of geometry for this procedure, as well as certain materials to prove your identity.

What’s the difference between identities and algebraic expressions?

An algebraic expression is an expression that has both a variable and a constant. A variable in an expression can have any value. As a result, if the variable values change, the expression value can change. However, algebraic identity is equality that holds for all variables’ values.

List of Algebraic Identities:

The standard algebraic identities are:

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

a² – b² = (a + b)(a – b)

(x + a)(x + b) = x² + (a + b) x + ab

(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

(a + b)³ = a³ + b³ + 3ab (a + b)

(a – b)³  = a³ – b³  – 3ab (a – b)

a³+ b³ + c³– 3abc = (a + b + c)(a²  + b²  + c²  – ab – bc – ca)

Solved Example Questions on Algebraic Identities:

Q.1. Find the product of (x+2)(x+2) using standard algebraic identities.

Ans: We can write (x+2)(x+2) as (x+2)².

By using the identity: (a+b)² =a² +2ab+b²

We get by adding the values of x=a and y=2 together.

⇒(x+2)² =x²+2²+2*x*2

⇒(x+2)²=x²+4+4x

Hence, the value of (x+2)(x+2) is x²+4x+4.

Q.2. Factorise 25x² +16y² +9z² –40xy+24yz–30zx using standard algebraic identities.

Ans:

Given: 25x² + 16y² +9z² –40xy+24yz–30zx

⇒5²x² + 4²y² +3²z²–40xy+24yz–30zx

⇒(–5x)² +(4y)² +(3z)² + 2×(–5x)×4y + 2×4y×3z + 2×(–5x)×3z

By using the identity: (a+b+c)2 = a² + b² +c² + 2ab + 2bc + 2ca

By putting the value of a=–5x,b=4y and c=3z

⇒(–5x+4y+3z)²

Hence, the factors of 25x²+16y²+9z²–40xy+24yz–30zx are (4y+3z–5x)(4y+3z–5x).

Q.3. Expand (x–3y)³ using standard algebraic identities.

Ans:

Given: (x–3y)³

After using the identity: (a–b)³ = a³ – b³ –3ab(a–b)

By putting the value of a=x and b=3y, we get,

(x – 3y)³=x³–(3y)³ –3(x)²(3y)+3(x)(3y)²

⇒x³ – 27y³ – 9x²y+ 27xy²

Conclusion:

An algebraic expression or equation is a statement that is only about math. Constants, variables, and exponents make form an algebraic equation. An equation cannot be called an identity if the values of the variables change and the equality becomes invalid. Students benefit from knowing and understanding these identities as they study mathematical techniques. It will also allow them to improve their proficiency in using these processes in algebraic manipulations and problem-solving.