Complex numbers are important to mathematics. These are numbers that can be represented in a+ib format, where a, b are real numbers, and i is the imaginary number. The value of i is (√-1). For example, we take 2+4i, then 2 is the real number, and 4i is the imaginary number. In this article, we look at the algebra of complex numbers.
Problems and Solutions
Question 1:
Simplify the equations and answer correctly.
- (4 + 3i) – (9 – 6i)
- (3 – 5i) (12 + 11i)
- (- 3 – 5i) / i
- 8i(10+2i)
Solution:
a. (4 + 3i) – (9 – 6i)=
-5 + 9i
b. ( 3-5i) (12+11i)
=36+33i-60i- 55i2
Taking i² =-1
=36- 27i -55 (-1)
=91-27i
c. (- 3 – 5i) / i
=(3+5i)i=3i+5i2
= -5 + 3i
d. 8i(10+2i)
=80i+ 16i²
Taking i²= -1
=80i-16
Question 2:
Find the value of (a + bi)(a – bi)
If (a+ bi) / i = ( 6 + 8i ) given x and y are real
Solution:
According to the question,
(a + bi) / i = ( 6 + 8i )
(a + bi) = i(6 + 8i) = –8 + 6i
(a + bi)(a – bi) = (-8 + 6i)(-8 +6i)
=64 + 36 = 100
Question 3:
Suppose the polynomial
P(z) = z⁴ + a z³ + b z²+ c z + d
where a, b, c and d are real numbers.
Determine the value of a, b, c and d if two zeros of polynomial P are the following complex numbers: 3 – i and 4 – i.
Solution:
The coefficients of given polynomial P are said to be real.
Then the complex conjugate to the given zeros are also zeros of P.
Therefore,
X(z) = (z – (3 – i))(z – (3 + i))(z – (4 – i))(z – (4 + i)) =
= z4– 14 z3 + 75 z2 +22 z + 170
Hence: a = -14, b = 175, c = 22 and d = 170.
Question 4:
Take the following equation
z2 + 2z + 2 = 0
Find the values of z using quadratic equations.
Solution:
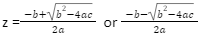
Here a=1 b=2 and c=2 putting values in above equation give
z=-1+i or -1-i
Question 5:
Look at the given complex number
z = -2 + 7i
The given equation root to the equation mentioned below:
z3 + 6 z2 + 61 z + 106 = 0
Determine the real root of the equation.
Solution:
We have been given z = -2 + 7i
This equation is a root of the equation
And all the coefficients in the terms of the equation are real numbers, then z’, the complex conjugate of z, is also a solution.
So to find z3 + 6 z2 + 61 z + 106 = 0
= (z – (-2 + 7i))(z – (-2 – 7i)) q(z)
= (z2 + 4z + 53) q(z)
q(z) = [ z3 + 6 z2 + 61 z + 106 ] / [ z2 + 4z + 53 ] = z + 2
Z + 2 is a factor of z3 + 6 z2 + 61 z + 106
So, z = -2, which is the real root of the equation provided.
Question 6:
(5 + 3i)z + (9 – 3i)z’ = -3 + 11i Determine all complexes that satisfies these conditions,
where z’ and z are conjugate of each other.
Solution:
To determine these numbers, let us assume z = x + yi x and y are real numbers.
The complex Z can be formed in terms of a and b as follows: z’= x – yi.
Write the values of z and z’ in the given equation
(5 + 3i)(x+iy) + (9 – 3i)(x-iy) = -3 + 11i
Expand and separate real and imaginary parts.
(5x – 3y + 9x – 3y) + (5y + 3x – 9y – 3x )i = -3 + 11i
Two complex numbers are equal if their real parts and imaginary parts are equal. Group like terms.
14a – 6y = -3 and – 4y = 11
Solve the system of the unknown a and b to find:
b = -11/4 and a = -39/28
z = -39/28 – (-11/4)i
Question 7:
In the complex number 2 + 4i is one of the roots to the quadratic equation x2 + bx + c = 0, where b and c are real numbers.
a. determine b and c
b. find the second root and check it.
Solution:
As we are given that b and c are real numbers so roots should be conjugate pairs of each other.
If one root is 2+4i then other will be 2-4i
So given equation can be written as (x-(2+4i))(x-(2-4i))
X2-4x+20
Value of b=-4 and value of c=20
b)We found out the second root as 2-4i
Putting this root in original equation
(2-4i)2-4(2-4i)+20
=4-16-16i-8+16i+20=0
Question 8:
Find all complex numbers of the form z = a + bi in the given equation where a and b are real numbers such that z z’= 25 and a + b = 7
where z’ is the complex conjugate of z.
Solution:
z z’ = (a + bi)(a – bi)
= a² + b² = 25
a + b = 7 gives b = 7 – a
Add values above in the equation a²+ b² = 25
a²+ (7 – a)²= 25
Now solve the mentioned equation for a and use b = 7 – a and determine the value of b.
a = 4 and b = 3 or a = 3 and b = 4
z = 4 + 3i and z = 3 + 4i have the property z z’ = 25.
Conclusion
This article explains the algebra of complex numbers and the algebraic form of complex numbers. Complex numbers are a combination of a real number and an imaginary number. One part of a complex number is real, while the other part is imaginary.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




