Profile
Settings
Refer your friends
Sign out
Integration means adding values on a big scale when a general addition operation is impossible. However, there are various methods of integration used in mathematics to integrate functions.
Integration and differentiation are inverse functions that are analogous to addition and subtraction and multiplication and division. Anti-differentiation or integration is the technique of locating functions whose derivative is known.
Different integration strategies used to find an integral function makes evaluating the original integral easier. Let us take a closer look at the various ways of integration, such as integration by parts, substitution and partial fractions.
Methods of Integration
Here are the common methods of integration.
Integration by Substitution
This method is a way of evaluating integrals and antiderivatives in calculus. It is also referred to as u-substitution or change of variables. It is the inverse of the formula for differentiating, akin to using the chain rule “backwards.”
Integration by Parts
Integration by parts or partial integration is a calculus procedure that finds the integral of a product of functions in terms of the product of their derivative and antiderivative. It is useful to convert the antiderivative of a product of functions into a derivative that is easier to solve.
The rule can be considered a more comprehensive product differentiation rule.
Integration by Partial Fractions
A rational fraction is one with a polynomial numerator and denominator. Suppose you express this fraction as a sum of a polynomial in one or more fractions with a simpler denominator. Such an algebraic operation denotes the partial decomposition or expansion of a rational fraction.
Integration Using Trigonometric Identities
We can use trigonometric identities to assess several integrals involving trigonometric functions. Trigonometry allows us to express the integrals differently, making integration easier. We use trigonometric identities to integrate for, e.g. sin2x, cos2x and sin3x functions.
Integration of Some Special Functions
The following are the most important types of integration of some special functions:
The Gamma Function
The gamma function is a mathematical function used to calculate the value of a number. The gamma function (represented by the Greek capital letter γ) is a regularly used extension of the factorial function to complex numbers in mathematics.
Except for non-positive integers, the gamma function is defined for all complex numbers.
The Functioning Beta
Beta functions, also known as Euler integrals of the first kind, are special functions. It is generally written as B(x, y), where x and y are both positive real values.
B(x, y) = B(y, x)
The term “special functions” is used in mathematics, and some functions exist as integral or differential equation solutions.
Functions of a Parabolic Cylinder
A parabolic cylinder is a three-dimensional quadratic surface (or quadric surface) in mathematics, especially in analytical geometry. It is defined by the equation:
x2 + 2ay = 0
In other words, a parabolic cylinder is one whose directrix is a parabola.
Integration with the Help of Trigonometric Identities
When the integration of functions includes trigonometric functions, we use trigonometric identities. It simplifies the function so that one can integrate it easily.
Some trigonometric identities are as follows:
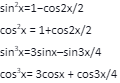
Integration by Partial Fraction
We already know that we can express a Rational Number as p/q. Here, p and q both are integers. Note that q is not equal to zero. Similarly, we can express a rational function as two polynomials’ ratios. And we can represent these ratios as partial fractions: P(x)/Q(x), where Q(x)≠0. In general, we can find a total of 2 types of partial fractions:- Proper partial fraction: If the numerator degree is lower than the denominator degree, then the type of partial factor found is defined as a proper partial fraction.
- Improper partial fraction:
