Arrhenious equation

Arrhenius equation

Introduction

The Arrhenius equation is an integral part of physical chemistry. The formula of the Arrhenius equation is dedicated to showing the temperature reliance of rates of reaction. 

In 1889, Svante Arrhenius formulated the equation. It depends on the Dutch chemist Jacobus Henricus van ‘t Hoff’s work, who formulated the van ‘t Hoff equation based on the equilibrium constants’ temperature dependency.

This Arrhenius equation contains a wide application range in deducing chemical reactions rates. Also, it plays a significant role in calculating the energy of activation. 

If we know the rate constant, we may use the Arrhenius equation to determine activation energies and vice versa. It also mathematically represents the preceding relationships: when the activation energy term Ea grows, the rate constant k falls, and the rate of response decreases.

Describe the Arrhenius Equation

The Arrhenius equation refers to an expression connecting a chemical reaction’s rate constant, A factor (pre-exponential factor), and the absolute temperature. 

 It gives insights into the reliance of reaction rates over the absolute temperature. 

The formula for the Arrhenius equation is:

K= Ae (-Ea/RT) ( Arrhenius equation calculator)

• k = reaction’s rate constant 
• A = pre-exponential factor 
• e = natural logarithm base (Euler’s number)
• Ea = chemical reaction’s activation energy 
• R = universal gas constant
• T = absolute temperature linked with the reaction 

For understanding the derivation equation of the Arrhenius equation formula in a more exploratory manner, you can utilise the Arrhenius equation graph. 

 Arrhenius Equation for Catalysts

 The catalyst’s job is to decrease a reaction’s activation energy requirements. Thus, the downward activation energy can be rearranged to the Arrhenius equation. It helps in obtaining the catalyzed reaction’s rate constant.

 The Arrhenius equation’s exponential portion (-Ea/R.T.) reports an increase in the rate constant value with any activation energy decrease. As the chemical reaction rate depends on the reaction’s rate constant, the reduction in activation energy yields an exclusive increment in the rate of reaction.

 Furthermore, uncatalysed reaction rates get more influenced by temperature in comparison to catalysts’ reactions rates.

The reason behind this is the placing of the exponential term (-Ea) at the numerator. And the positioning of absolute temperature (R.T.) at the denominator. Due to the catalyst reaction’s low activation energy value, rate constants get more affected by temperature than uncatalyzed reactions.

 Pre-Exponential Factor (A) and the Arrhenius equation 

Arrhenius equation contains a letter A denoting the frequency or pre-exponential factor. 

The factor relates to the process of collisions among the molecules. It is also explained by collisions’ frequency of molecules. Such molecules contain adequate energy to provoke a chemical reaction.

The equation for the pre-exponential factor:

A = ⍴Z

 Z = collisions’ frequency factor

⍴ = steric factor 

The value of A is experimentally derived as it infers various values across distinct reactions. Additionally, it also depends on the reaction’s temperature. The units of A depend on the reaction order. 

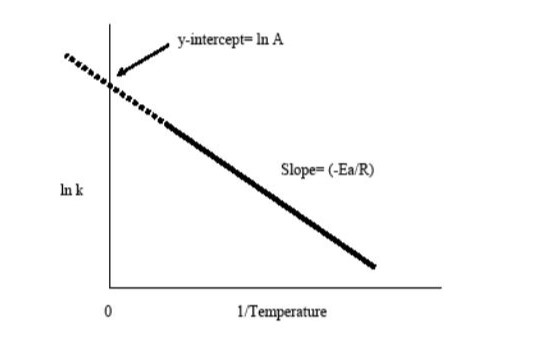
Plotting the logarithm

Plotting the logarithm of something like the rate constant, k, against the inverse temperature, 1/T, yields the Arrhenius plot. The resultant downward sloping line can be used to locate the missing Arrhenius equation components. The value for A is obtained by extrapolating the line back to the y-intercept. The negative activation energy divided by the gas constant, R, determines the line’s slope. As a matter of thumb, the pace of most biological and chemical processes doubles every 10 degrees Celsius rise in temperature.