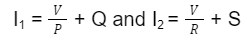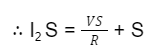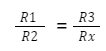Profile
Settings
Refer your friends
Sign out
The Wheatstone Bridge is a basic circuit used for measuring unknown resistance in small amounts. The measurement of resistance is done by connecting the unknown value resistor with three resistors of known value in a quadrilateral arrangement. Then voltage is applied between one pair of opposite corners, and a galvanometer is connected to the other pair of opposite points and calculations are made. Now that we know what Wheatstone Bridge is, let’s understand its principle theory and proof.
Next, let’s learn, what is the balanced condition of Wheatstone Bridge?
What is the Balanced Condition of Wheatstone Bridge?
A balanced Wheatstone Bridge is one where no current flows through the coil, and thus, the potential difference across the galvanometer is zero. This condition takes place when the potential differences between points AB and points AD are equal. Similarly, the potential differences between points BC and CD also remain the same.
Consider this Wheatstone Bridge circuit where the resistances P and R are in series connection with each other, and so are S and Q. But the combination of P and R resistances is in a parallel connection with resistances S and Q. Currents I1, I3, I2, and I4 flow through resistors P, Q, R, and S, respectively.
In this circuit, the current I enters into the galvanometer and gets divided into I1 and I2. If the galvanometer indicates a zero value, it means that these currents share the same magnitude. Such a condition is called a balanced Wheatstone Bridge condition.
The same can be mathematically indicated for currents I1 and I2 as follows:
Now, in the circuit, the potential of point B wrt point C is the voltage drop across Q. In this scenario, the equation will be
Similarly, the potential of point D with respect to C is the voltage drop across the resistor S, then the equation is
From the above two equations, we get
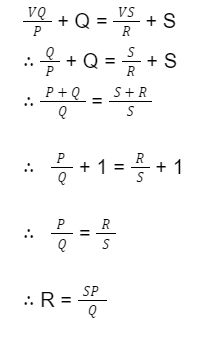
The Wheatstone Bridge Theory of Operation
The figure given below shows a variation of Wheatstone bridge, where the resistance R4 has been replaced by an unknown resistance Rx. Rx is attached to the sensing arm between the points BD, and R3 has been adjusted to give the Wheatstone Bridge its balanced condition. Now, the circuit is expected to bring zero output on the galvanometer as per the Wheatstone Bridge principle.
Thus, when the bridge is balanced, the resistances on the circuit can be indicated as:
Now, let’s explore the wheatstone bridge balance equation for unknown resistance Rx. Here, the values of resistors R1 and R2 are known or preset.
It can be calculated as shown below:
Where:
Vout indicates the total Voltage output.
Vc and Vd are voltage outputs at points C and D respectively.
R1, R2, R3, and R4 (Rx) are the four resistors as indicated in the image.
Whereas Rc and Rd are the resistances at points C and D.
This derivation proves that when R4 is replaced by an unknown resistance Rx in balanced condition, the value of Rx comes the same as the value of R4.
Now, this is only possible if the galvanometer reading is zero, since the two resistances are connected with each other parallelly.
Thus, the balanced condition of the Wheatstone Bridge is proven by a zero galvanometer reading. This is called the proof of the Wheatstone Bridge principle.
Conclusion
This lesson teaches us the arrangement of Wheatstone Bridge Circuit along with its principle. Remember the formula of the balanced Wheatstone Bridge condition, as it is important for all Wheatstone Bridge calculations. Further, you can refer to the frequently asked questions below to prepare for MCQs on the topic.
