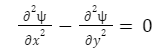What Is Streamline Flow?

The streamline function is a scalar function of space and time that provides the velocity component at sharp angles to any direction when its partial derivative is calculated with respect to that direction. The streamline flow is also called laminar flow. It is exclusively defined for two-dimensional flow and is indicated by Ψ(Psi). In material terms, steady flow can be defined as,

The velocity components in cylindrical coordinate in terms of streamline function are given as,

Where u_r is the radial velocity and u_θ is the tangential velocity.

The continuity equation for two-dimensional flow will be given as ,

Put the values of u and v, then we get,

Hence, existence of means a possible case of fluid flow. The flow may be rational or irrotational. The rotational component ω_z is given as,

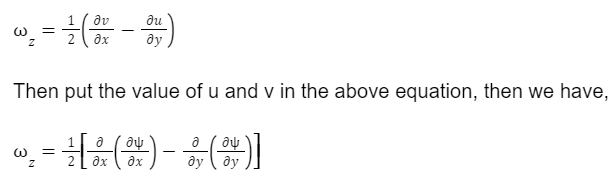
Where Ψ  is the Laplace equation.

For example – A streamline function is given as Ψ =5x-6y. Calculate the velocity, magnitude, and direction of the resultant velocity at any point.

Solution:

Given, ψ =5x-6y

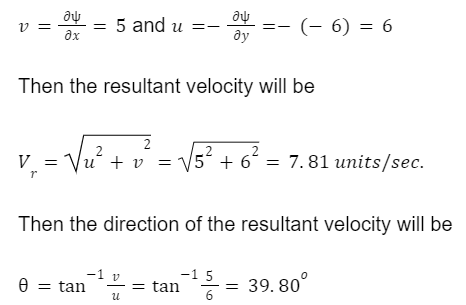
The properties of a streamline function () are as follows;

1. If the stream function () exists, it indicates a possible scenario of rotational or irrotational fluid flow.

2. It is a conceivable case of an irrotational flow if the stream function () fulfils the Laplace equation.

Advantages of the streamline flow

1. The energy loss in the streamline flow is very less.

2. The streamline flow reduces the energy consumption in pumping of water.

3. There is a little friction between the liquid layers.

Laminar flow and turbulent flow

Laminar flow – When a fluid flows layer by layer, this type of flow is called laminar flow. Molecules in one layer do not mix with those in other layers of the fluid. The flow is also called the streamline flow or viscous flow. In the flow, viscosity is significant.

Turbulent flow – When a layer of a fluid gets mixed up with the other layer of the fluid, it is called turbulent flow.In the flow, a particle of the fluid moves in an irregular manner.

Difference between streamline flow and turbulent flow

Relation between the streamline function and velocity potential function

We know that the velocity potential function is given as,

We know that the streamline function is given as,

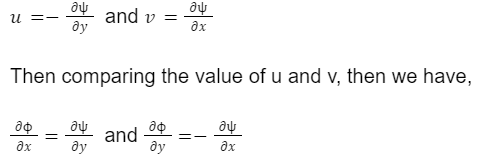
For example – The velocity potential function is given as Φ =2xy. Find the velocity at the point (3, 4). Define the streamline function at point P.

Solution:

Given, Φ = xy

1. The velocity components in the direction of x and y are,

At the point P(3, 4), we have, 

u=-2×4=-8 units/sec

v=-2×3=-6 units/sec

The velocity at point P will be, 

=-6i-8j

The resultant velocity at point P will be,

The constant of integration C is not a function of y but it can be a function of x. Then differentiate the above equation with respect to x, we have,

Conclusion

It is very important to know the flow is streamline or turbulent. If the flow is streamline, then all the theories of laminar are to be applied for the designing. And if the flow is turbulent, then all the theories of turbulence are to be applied for the design.