Equivalent Resistance Formula

Equivalent Resistance Formula 

When current is passed through any material, some opposition is also produced. This opposition to current flow is called the resistance of that material. Let us know more about it.

Definition 

Equivalent resistance is the calculation of combined value of resistance, which are either connected parallel or in series with each other, is done. 

The circuit is designed in two ways:

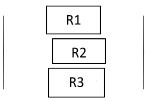
1. Parallel

2. Series

Resistance shows how much energy one requires when you move the current that flows through your gadgets. For a large amount of energy required the resistance is additionally high as well. The equivalent resistance is calculated in order to find the resistance of a single resistor that can replace the whole network of resistors as one, so that for a specific applied voltage V you get a similar current I as you were getting for that whole system previously.

Resistance is denoted by R and its Unit is Ohm.

Formula

For parallel network:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

For a Series Network:

R = R1 + R2 + R3 + … + Rn

Where R1, R2, R3….,Rn are given resistors and R is the Equivalent Resistance.

Some Examples

Let us see some examples below for a proper understanding of this concept.

Ex.1. Find the equivalent resistance of a circuit with a resistance of 2Ω, 10Ω, and 30 Ω, all connected to each other in series.

Solution: 

R1 = 2 Ω

R2 = 10 Ω

R3 = 30 Ω 

For series the formula used is:

R = R1 + R2 + R3 + … + Rn

R = 2 + 10 + 30

R = 42 Ω

Ex.2. What will be the equivalent resistance if three resistors with a resistance of 20 Ω, 3 Ω, and 5 Ω are connected in parallel. 

Solution:

Given: R1 = 20 Ω ,   R2=3 Ω,   R3=5 Ω

For Parallel,
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

1/R = 1/20 + 1/3 + 1/5

1/R = 89/180

R = 2.02

Ex.3. What will be the resistance of two resistors in parallel with equal resistance, if the equivalent resistance is 4 Ω.

Solution:

Given

Resistors have the same resistance, let’s say r.

Equivalent resistance = 4 Ω

So, with the help of following formula;
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

1/4 = 1/r + 1/r

1/4 = 1/2r

r = 4/2

r = 2 Ω

Hence, each resistor is of 2 Ω.