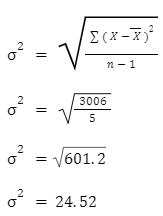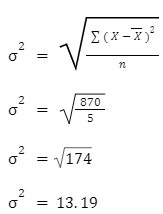Profile
Settings
Refer your friends
Sign out
Standard Deviation Formula
What is a standard deviation and What does it do? There is no exact way of explaining a standard deviation other than understanding the formula used to calculate it. However, insight into the concept of standard deviation can be gained by learning the way in which it is used and computed.
Understanding Standard Deviation
The square root of the variance is called the standard deviation. It is often abbreviated to SD. The standard deviation is denoted by ””. The standard deviation has been assigned as a measure of variability. It is applied as a separate entity well as a part of other analyses, such as computing confidence intervals and hypothesis testing.
The standard deviation is used to tell how far on average any data point is from the mean. The smaller the standard deviation, the closer the data points are on average to the mean. When the standard deviation is large, the data points are more widely spread out on average from the mean. The standard deviation is computed to measure the avg. distance from the mean.
What is the Standard Deviation Formula?
Following is the formula to compute standard deviation:-
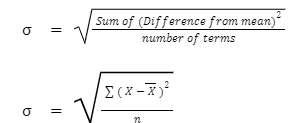
Where:σ = Standard Deviation
X = Values or terms
X = Arithmetic Mean
n = Number of terms
Solved Examples
Calculate the standard deviation of the following test data.
Test Scores: 22, 99, 102, 33, 57
Test Score (X) | Difference from the mean (X-X) | Square of difference from the mean (X-X)2 |
22 | -18 | 324 |
78 | 38 | 1444 |
10 | -30 | 900 |
33 | -7 | 49 |
57 | 17 | 289 |
X = 40 | ( X – X )2 = 3006 |
Thus, the standard deviation of the given test scores is 24.52
The data set below gives the prices (in dollars) of a few items at a departmental store.
35, 50, 60, 60, 75
Items (X) | Difference from the mean (X-X) | Square of difference from the mean (X-X)2 |
35 | -21 | 441 |
50 | -6 | 36 |
60 | -4 | 16 |
60 | -4 | 16 |
75 | 19 | 361 |
X = 56 | ( X – X )2 = 870 |
Thus, the standard deviation of the given items is 13.19
