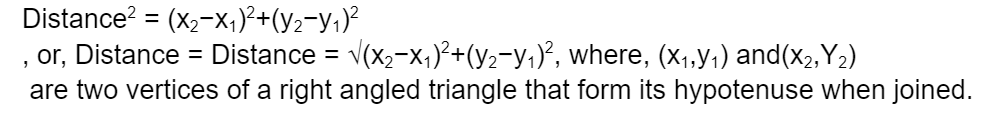Distance Formula

Any distance formula, as its name suggests, gives the distance (the length of the line segment). For example, the distance between two points is the length of the line segment connecting them. We use the Pythagoras theorem to derive the formula for distance between two points in a two-dimensional plane which can be extended to find the distance between two points in a three-dimensional plane as well. There are different types of distance formulas in coordinate geometry.

• Distance between two points in a 2D plane
• Distance between two points in a 3D plane
• Distance from a point to a line in 2D
• Distance between two parallel lines in 2D

Types of Distance Formula

• distance between two points,
• distance between a point to a line, 
• distance between two parallel lines,
• distance between two parallel planes, etc

Distance formula for distance between two points

The distance between two points is derived by using the Pythagoras theorem.

The distance formula which is used to find the distance between two points is also known as the Euclidean distance formula. To derive the formula, let us consider two points in 2D plane A(x1,y1), and B(x2,y2).

Assume that ‘d’ is the distance between A and B. Distance formula for distance between a point to a line.

    Distance formula for distance between two parallel lines 

In this section, we will see the distance formula for the distance from a point to a line.

The distance formula to calculate the distance from a point to a line is the length of the perpendicular line segment that is drawn from the point to the line. Let us consider a line L in a two-dimensional plane with the equation ax + by + c =0 and consider a point

P(x1,y1).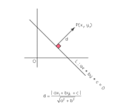      

Distance formula for distance between two parallel planes

We know that the slopes of two parallel lines are always the same. So we can assume the two parallel lines to be L1: ax +by + c1= 0 and L2:  ax + by + c2= 0 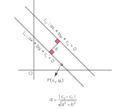   Applications of Distance Formula

The distance formula has numerous applications in other areas of mathematics and also in many real-life situations. Some of the uses of the distance formula are as follows.

• The distance of any point from the origin can be calculated using the distance formula.
• The complex number is represented in the arg-and plane, and the formula to find the magnitude of a complex number has been derived from the distance formula.
• The distance formula can also be used to find the distance between two points in three-dimensional and also in n-dimensional planes.