In 2D geometry, a straight line is defined as the locus of a moving point P (h, k) such that the point P is always collinear with the two given fixed points, say A (x1, y1) and B (x2, y2). The slope of a straight line, also known as gradient, is defined as the angle of inclination, say θ, made by the line with the positive X-axis in a 2D plane and is denoted by m.
The slope of a straight line is expressed as –
Slope = gradient = m = tan θ = (Perpendicular / Base) = /\Y / /\X = [(y2 – y1) / (x2 – x1)].
The concept of a straight line and slope of a straight line
Straight-line – An Overview
A straight line is defined as a geometrical shape with no breadth and endpoints. It is extendable in both directions.
In 2D geometry, a straight line is defined as the locus of a moving point P (h, k) such that the point P is always collinear with the two given fixed points, say A (x1, y1) and B (x2, y2).
Depending on the type of information given, the equation for a straight line can be expressed in various forms such as General form, Point-slope form, Two-points form, Slope-Intercept form, Intercept form, and Normal or Perpendicular form.
To find the Point-slope form and/or Slope-Intercept form of the equation of a line, it is imperative to know the value of the slope of that line. For this very purpose, we will now focus on finding the slope from two points.
The slope of a straight line
The slope of a straight line, also known as gradient, is defined as the angle of inclination, say θ, made by the line with the positive X-axis in a 2D plane and is denoted by m. That is, m = tan θ.
The slope of a straight line is expressed as –
Slope = gradient = m = tan θ = (Perpendicular / Base) = /\Y / /\X = [(y2 – y1) / (x2 – x1)].
The slope of a straight line is a numerical value that can also be defined as the ratio of change in the vertical distance of the points to the change in the horizontal distance of the points. That is, m = /\Y / /\X = [(y2 – y1) / (x2 – x1)].
The slope of a straight line can also be called the steepness of that line.
Derivation to find slope from two points
There are two cases depending on the angle of inclination from which we can derive the formula to find slope from two points.
We know that m = tan θ.
Let us assume two points, P and Q, on a line l whose coordinates are P (x1, y1) and Q (x2, y2).
The line l is non-vertical and whose inclination angle is θ, where θ may be either acute or obtuse but not 90o.
For obvious reasons to find slope from two points when the coordinates of both points are given, x1 ≠ x2.
We now draw a perpendicular from l to the x-axis represented by QR and a perpendicular from point P to QR represented by PM.
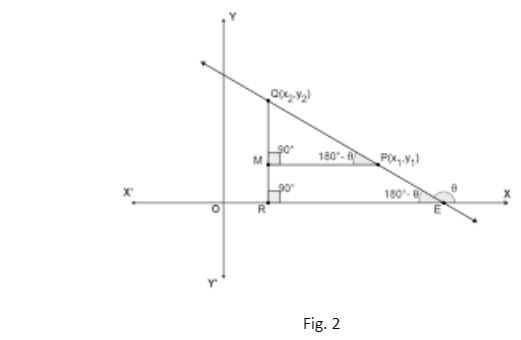
Consider the below-given figures for reference where the θ in fig. 1 is acute, and the θ in fig. 2 is obtuse.
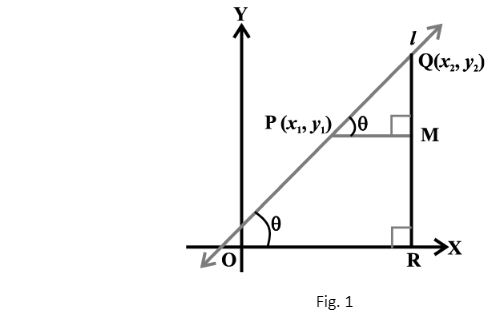
CASE 1: When θ is acute. (Refer to fig. 1).
From the given figure, we can see that / MPQ = θ.
Thus, the slope of the given line l = m = tan θ = (Perpendicular / Base).
Thus, in /\MPQ, tan θ = (Perpendicular / Base) = QM / PM = [(y2 – y1) / (x2 – x1)].
Hence, we have obtained the relation m = [(y2 – y1) / (x2 – x1)], when angle of inclination is acute.
CASE 2: When θ is obtuse. (Refer to fig. 2).
From the given figure we can see that / MPQ = (180o – θ).
The above expression can be rewritten as –
θ = (180o – / MPQ).
Then,
tan θ = tan (180o – / MPQ).
tan θ = – tan (/ MPQ).
tan θ = – (QM / PM) = – [(y2 – y1) / (x1 – x2)] = [(y2 – y1) / (x2 – x1)].
We know that the slope of the given line l = m = tan θ.
Thus, m = [(y2 – y1) / (x2 – x1)].
Hence, we have obtained the relation m = [(y2 – y1) / (x2 – x1)], when angle of inclination is obtuse.
Conclusion
By the end of this precise and concise article on Functions – Find Slope From Two Points, we have understood and grasped the concepts of slope of a straight line and derived the formula to find slope from two points when the coordinates of both points are given.
We have learnt that,
A straight line is defined as the locus of a moving point P (h, k) such that the point P is always collinear with the two given fixed points, say A (x1, y1) and B (x2, y2).
The slope of a straight line, also known as gradient, is defined as the angle of inclination, say θ, made by the line with the positive X-axis in a 2D plane and is denoted by m.
The slope of a straight line is expressed as –
Slope = gradient = m = tan θ = (Perpendicular / Base) = /\Y / /\X = [(y2 – y1) / (x2 – x1)], regardless of whether θ is acute or obtuse.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






