Ampere’s Circular Law
The formula for Ampere’s circuital law are as stated below |
| Description |
Formula |
| Ampere’s circuital law |
\int_{\ }^{\ }B.dl=μ°I
Here μ°= permeability of free space=4Π×10-15NA-2
B = Magnetic field
I = enclosed electric current by the path |
| Ampere’s law (integral form) |
\int_{\ }^{\ }B.ds=μ°Ienclosed
Ienclosed= enclosed current by the surface |
| Field of a current-carrying wire: |
B=μ°/I2πr |
| Field of a solenoid |
BL=°NI
Here N: number of turns in the solenoid |
| Field inside a thick wire |
\int B.ds=μ°I
And
B=μ°I.r2/πR2 |
| Field of the toroid |
B=μ°NI/2πr |
| Force between two parallel current carrying wires |
F_\frac{A}{B}=μ°IAIB2πr
IA,IB= Current carrying by wires A and B |
Capacitance formula
The formula for capacitance are as stated below |
| Description |
Formula |
| Capacitance of a parallel plate capacitor in terms of charge and potential difference |
C=Q/V
Here, C is the capacitance of the capacitor, Q is the charge stored and V is the potential difference between the plates. |
| Capacitance of a parallel plate capacitor in terms of surface area and distance between the plates |
C=\frac{\varepsilon_0A}{d}
Here, is the permittivity of free space and its value is 8.854×10-12m-3 Kg-1 s4 A2 is the surface area of the plates and d is the distance between the plates. |
| Capacitance of a spherical capacitor derivation |
To find the formula for capacitance of a spherical capacitor we will use the gauss’s law.
Let the charge on the spherical surface be , the radius of smaller sphere be and radius of the bigger sphere be .
Using gauss’s law, we can write:
\oint_{\ }^{\ }\ \vec{E}\cdot d\vec{A}=\frac{Q}{\varepsilon_0}
E\left(4\pi r^2\right)=\frac{Q}{\varepsilon_0}
E=\frac{Q}{4\pi\varepsilon_0r^2}
V=\frac{Q}{4\pi\varepsilon_0r} |
| The potential difference between the plates |
V_{ab}=V_a-V_b=\frac{Q}{4\pi\varepsilon_0}\left(\frac{1}{r_a}-\frac{1}{r_b}\right)
=\frac{Q}{4\pi\varepsilon_0}\frac{r_b-r_a}{r_ar_b}
Therefore, the capacitance will be:
C=\frac{Q}{V_{ab}}=\ 4\pi\varepsilon_0\frac{r_ar_b}{r_b-r_a} |
| Energy stored in capacitor |
● U=1/2 CV2
● U= Q2/2c
● U= QV/2
Here, U is the energy, C is the capacitance, V is the potential difference and Q is the charge stored. |
| Energy density of capacitor |
Energy density=\frac{1}{2}\varepsilon_0\varepsilon_rE^2
In vacuum:
Energy density= \frac{1}{2}\varepsilon_0E^2
Here, Eo is the permittivity of free space, is the relative permittivity and E is the electric field. |
| Capacitance per unit length of a cylindrical capacitor |
Capacitance per unit length= 2ΠEo/In(b/a)
Here, Eo is the permittivity of free space, b is the radius of outer cylinder and a is the radius of inner cylinder. |
| Electric field intensity |
The formula for electric field intensity between the plates is given as:
E= σ/Eo=V/d
Here, σ is the surface charge density, V is the potential difference and d is the distance between plates. |
| Redistribution of charge when two charged capacitors are connected in parallel |
Let us assume a capacitor with capacitance with initial charge and capacitor with capacitance with initial charge .
The final charge on capacitor with capacitance will be:
Q’1=C1/C1+c2(Q1+Q2)
final charge on capacitor with capacitance will be:
Q’2=C1/C1+c2(Q1+Q2) |
| Equivalent capacitance when capacitors are connected in series |
\frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\ldots+\frac{1}{C_n}
Here, is the equivalent capacitance and are the capacitance of the capacitors. |
| Equivalent capacitance of the capacitors connected in parallel |
C_{eq}=C_1+C_2+C_3+\ldots C_n |
| Charging of capacitor |
q=q_0\left(1-e^{-\frac{t}{\tau}}\right)
Here, q is the charge on the capacitor at time t, is the time constant and is the charge on the capacitor at steady state. |
| Discharging of capacitor |
q=q_0e^{-\frac{t}{\tau}}
Here, q is the charge on the capacitor at time t, is the time constant and is the charge on the capacitor at steady state. |
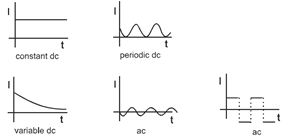 A current that changes its direction periodically is called alternating current (AC). If a current maintains its direction constant it is called direct current (DC).
A current that changes its direction periodically is called alternating current (AC). If a current maintains its direction constant it is called direct current (DC).
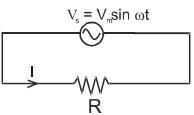 I=\frac{V_S}{R}=\frac{V_msin\omega t}{R}=I_msin\omega t
I_m=\frac{V_m}{R}
I_{rms}=\frac{V_{rms}}{R}
< p >=V_{rms}I_{rms}cos\phi=\frac{V_{rms}^2}{R}
I=\frac{V_S}{R}=\frac{V_msin\omega t}{R}=I_msin\omega t
I_m=\frac{V_m}{R}
I_{rms}=\frac{V_{rms}}{R}
< p >=V_{rms}I_{rms}cos\phi=\frac{V_{rms}^2}{R} I=\frac{\frac{V_m}{1}}{\omega c}cos\omega t
=\frac{V_m}{X_c}cos\ \omega t=I_mcos\omega t\
X_c=\frac{1}{\omega C\ } And is called capacitive reactance.
I=\frac{\frac{V_m}{1}}{\omega c}cos\omega t
=\frac{V_m}{X_c}cos\ \omega t=I_mcos\omega t\
X_c=\frac{1}{\omega C\ } And is called capacitive reactance.
 lc Leads by Vc by Π/2 , Diagrammatically it is represented as
lc Leads by Vc by Π/2 , Diagrammatically it is represented as
 Since, \phi={90}^0,
=V_{rms}I_{rms}cos\phi=0
Since, \phi={90}^0,
=V_{rms}I_{rms}cos\phi=0 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out



