JEE Physics Important Formulas Part -6

Faraday’s law formula

The formula for Faraday’s law are as stated below

Description

Formula 

Faraday’s first law

The first law of Faraday’s electromagnetic induction explains that when a wire is kept in a field that experiences a constant change in its magnetic field, then an electromagnetic field is developed. This phenomenon of development of the electromagnetic field is called an induced emf.

Faraday’s second law

1. It states that the emf induced in a conductor is equivalent to the rate at which the flux is linked to the circuit changes.

𝜀=−𝑑𝜙/𝑑𝑡

Where, 𝜀 = the emf or electromotive force

𝜙 = the magnetic flux

2. If there are N number of turns in the coil then the total magnetic induction in a coil is represented as 

𝜀=−𝑁( 𝑑𝜙/𝑑𝑡)

Magnetic flux

It is the integral (sum) of all of the magnetic fields passing through infinitesimal area elements dA.   

             ΦB=∫B∙dA 

The magnetic flux through a surface

The component of the magnetic field passing through that surface. The magnetic flux through some surface is proportional to the number of field lines passing through that surface. The magnetic flux passing through a surface of vector area A is      

       ΦB=BA=BA cosθ

Lenz’s Law

The direction of induced emf or current in the circuit is in such a way that it opposes the cause due to which it is produced. Therefore,

E=-N(dϕ/dt)

Induced emf   

Induced emf is given as
E = -N(dϕ/dt)

E = E = -N((ϕ_1- ϕ_2)/t)

Magnetic Flux

The magnetic flux through a plane of area dA placed in a uniform magnetic field B is given as

ϕ=∫B∙dA

Fluid mechanics & Properties of Matter Formula

The formula for fluid mechanics and properties of matter are as stated below

Description

Formula

Pressure

P=F/A

For hydraulic press:

F=A/a f

Here, P is the pressure, F is the force applied on bigger piston with area A and f is the force on the smaller piston with area a.

Angle made by liquid surface when container experiences an acceleration

tan θ =a_0/g
here, θ is the angle made by the liquid surface with the horizontal, a_0
is the acceleration of the container and g is the gravitational acceleration.

Continuity equation

According to the equation of continuity, the product of velocity and the area of cross section at any section in a tube is constant.

a_1 v_1=a_2 v_2

here, a_1 v_1
 are the area of cross section and velocity of fluid at section 1 and  a_2 v_2
are the area of cross section and velocity of the fluid at section 2.

Bernoulli’s equation

According to Bernoulli’s equation the total energy of liquid flowing through a tube is constant throughout the tube.

P/ρg+v^2/2g+Z=constant

Here, P is the pressure, is the density of the fluid, g is the gravitational acceleration, v is the velocity of the fluid and Z is the potential head.

The term(P/ρg)
is called pressure head, (v^2/2g) is called velocity or kinetic head and Z is called the potential head.

Speed of efflux

v=√(2gh/(1-(A_2^2)/(A_1^2 )))

Here, v is the velocity, g is the gravitational acceleration, h is the height,
A_2
is the area of hole andA_1 is the area of the vessel.

Stress

σ=FA
here, σ is the stress, F is the force and A is the area.

Strain

ε=ΔL/L
here, is the strain, ΔL is the change in length, and L is the initial length.

Young’s modulus

E=σ/ε

Or

E=FL/AΔL
here, E is the young’s modulus, F is the force, L is the initial length, A is the area of cross section and ΔL is the change in length.

Stoke’s law

F=6πηrv

Here, F is the drag experienced by the sphere, r is the radius of the sphere, η is the viscosity of the fluid and v is the velocity of the sphere.

Terminal velocity

v=2/9 ((r^2 (ρ-σ)g)/η)

Here, r is the radius of the sphere, is the density of the sphere, σ is the density of the fluid, g is the gravitational acceleration and  η is the viscosity of the fluid.

Magnetic Effect of Current formula

The formula for magnetic effect of current are as stated below

Description

Formula

Magnetic field due to a moving point charge

Magnetic field due to a moving point charge is given as

B ⃗=(μ_0 q(v ⃗×r ⃗ ))/(4πr^3 )

 μ_0= permeability of free space 

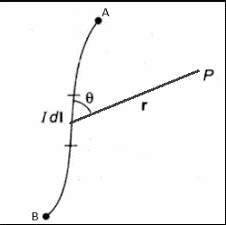
Biot Savart’s Law

dB∝(I ∙ dl ∙ sin θ)/r^2

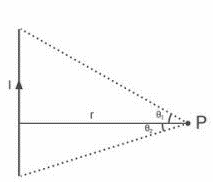
Magnetic field due to a straight wire

The magnetic field due to a straight wire is given as

B=(μ_0 I)/4πr (sinθ_1+sinθ_2 )

Magnetic field due to an infinite straight line

B = (μ_0 I)/2πr

Magnetic field due to a circular loop

At Axis (μ_0 (NIR^2))/(2〖(R^2+x^2)〗^(3/2) )

At centre  B=(μ_0 NI)/2r

Magnetic field on the axis of a solenoid

B=(μ_0 NI)/2 (cosθ_1-cosθ_2 )

Ampere’s Law

∮ B ⃗∙(dl) ⃗ = μ_0 l

Magnetic field due to a long cylinder

B=0,r<R

And 

B=(μ_0 NI)/2r ,r≥R

Magnetic force acting on a moving point Charge

(F ) ⃗=q(v ⃗×B ⃗ )

Magnetic force acting on a current-carrying

(F ) ⃗=I(l ⃗×B ⃗ )

Magnetic Moment of a current carrying loop

M= NIA

The torque acting on a loop

τ ⃗=M ⃗×B ⃗

Magnetic field due to single pole

B = (μ_0 m)/(2πr^2 )

Magnetic field on the axis of the magnet

B = (μ_0 2M)/(4πr^3 )

Magnetic field on the equatorial axis of the magnet

B = (μ_0 M)/(4πr^3 )

Magnetic field at the point P of the magnet