Profile
Settings
Refer your friends
Sign out
Current electricityThe formula for current electricity are as stated below |
|
| Description | Formula |
| Formula for current |
|
| Electric current in a conductor(wire) | I=nAeV_d v_d=λ/τ Here, n is the number of free electrons, A is the area of conductor, e is the charge of an electron, V_d is the drift velocity, λ is the linear charge density and τ is the relaxation time. |
| Potential difference using ohm’s law | V=IR Here, V is the potential difference, I is the current flowing through the conductor and R is the resistance offered by the conductor. |
| Resistance in terms of resistivity | R=ρl/A Here, ρ is the resistivity of the material of the conductor, l is the length of the conductor and A is the area of cross section of the conductor. |
| Change in resistance due to temperature | R=R_0 (1+αΔT) Here, R is the resistance, R_0 is the initial temperature, is the temperature coefficient of the resistivity and ΔT is the change in temperature. |
| Electric power | P=VI Here, P is the power, V is the potential difference and I is the current. Also, P=I^2 R P=V^2/R |
| Heat energy released due to current | H=VIt also H=I^2 Rt H=V^2/R t Here, H is the heat released in joules, V is the potential difference, R is the resistance, I is the current and t is the total time the current was flowing through the conductor. |
| Equivalent resistance when resistors are connected in series | Req=R_eq=R_1+R_2+R_3+⋯+R_n Here, R_eq is the equivalent resistance, R_1,R_2,R_3 are the resistance of the resistors. |
| Equivalent resistance when resistors are connected in parallel | 1/R_eq =1/R_1 +1/R_2 +1/R_3 +⋯+1/R_n |
| Potential difference when cells are connected in parallel | E_eq=((ε_1/r_1 +ε_2/r_2 +ε_3/r_3 +⋯+ε_n/r_n ))/(1/r_1 +1/r_2 +1/r_3 +⋯+1/r_n ) Here, ε_1,ε_2,ε_3 are the emf of the cells and r_1,r_2,r_3are the internal resistance of the cells. |
| Ammeter using galvanometer | To measure the maximum current I using a galvanometer, we need to connect a shunt resistance in parallel with the galvanometer. The value of the resistance is calculated as: S=(I_g R_g)/I Here, S is the value of shunt resistance, Ig is the current through galvanometer, Rg is the resistance of the galvanometer and I is the maximum current to be measured. |
| Voltmeter using galvanometer | To measure a potential difference using a galvanometer, we need to connect a series resistance with it. The value of the resistance that needs to be connected is: Rs=VIg-Rg Here, V is the maximum potential difference to be measured, I_g is the current through galvanometer andR_g is the resistance of the galvanometer. |
Electric current formulaThe formula for electric current are as stated below |
|
| Description | Formula |
| Electric current | I=q/t=ne/t Where I= strength of current; q-charge; t- time |
| Resistance |  |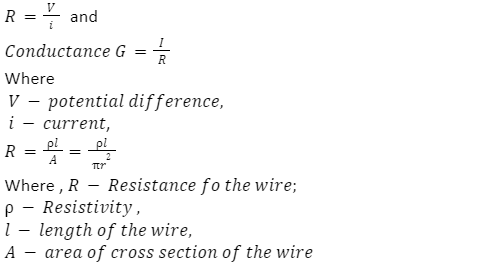
| Variation of resistance with the temperature | R_T=R_° [1+α(t)] →α=(R_(t-) R_(° ))/(R_° (t) ) l°∁ α=((R_1-R_2 ))/(R_1 (t_2-t_1 ) ) l °∁ Here, R = resistance at temperature t°∁ R° = resistance at temperature 0°∁= temperature coefficient of resistance |
| Conductivity | Reciprocal of resistivity. σ=1⁄ρ Where – σ -conductivity, ρ -resistivity |
| Terminal voltage | Case-1: When battery is delivering current V=E-ir or i=E/R+r Where V -terminal P.d, E – emf of the cell, r -internal resistance of the cell, R- external resistance. Case 2: when battery is charging V=E+ir |
| Kirchhoff’s laws | Kirchhoff’s First laws: ∑_ ^ i=0 at any junction. Kirchhoff’s second law: ∑_ ^ iR=0 in a closed circuit. |
| Metre Bridge |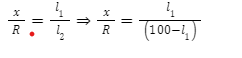 
Where x – unknown resistance of given wire, R-resistance in the resistance box, l1-balancing length from left end of the bridge to Jockey.
|
| Potentio Meter | Emf of cell in the secondary circuit
E_s=Iρl
|
Electromagnetic Induction FormulaThe formula for electromagnetic induction are as stated below |
|
| Description | Formula |
| Magnetic Flux | The magnetic flux through a plane of area dA placed in a uniform magnetic field B is given as ϕ=∫ B ⃗∙dA ⃗ When the surface is closed, then magnetic flux will be zero. This is due to magnetic lines of force are closed lines and free magnetic poles is not exist |
| Electromagnetic Induction: Faraday’s Law | First Law: Whenever magnetic flux linked with a circuit changes with time, an induced emf is generated in the circuit that lasts as long as the change in magnetic flux continues. Second Law: According to this law, the induced emf is equal to the negative rate of change of flux through the circuit. E = -dϕdt |
| Lenz’s Law | The direction of induced emf or current in the circuit is in such a way that it opposes the cause due to which it is produced. Therefore, E = -dϕ/dt |
| Induced emf | Induced emf is given as E = -N(dϕ/dt) E = -N((ϕ_1- ϕ_2)/t) |
| Induced Current | Induced Current is given as I=E/R = N/R(dϕ/dt)= N/R((ϕ_1- ϕ_2)/t) |
| Self – Induction | Change in the strength of flow of current is opposed by a characteristic of a coil is known as self-inductance. It is given as ϕ=LI Here, L = coefficient of self – inductance Magnetic flux rate of change in the coil is given as Idϕ/dt = L dl/dt=-E |
| Mutual – Induction | Mutual – Induction is given as e_2=(d(N_2 ϕ_2)/dt = M (dl_1)/dt Therefore, M=(μ_0 N_1 N_2 A)/l |
JEE Physics Important Formulas Part 3
In this article we will go through physics quick formula revision for JEE 2022. Find the important formulas of Current electricity, Electric current and Electromagnetic Induction.
