The Wheatstone bridge is a very useful device. It is used to measure resistances that are not known. It uses a principle that lets it measure the unknown resistance with the help of known resistance. Therefore, a Wheatstone bridge can be defined as a device used to calculate medium or minimum resistance by comparing it with known resistance. The measurement of the Wheatstone bridge is accurate and reliable. The Work of Wheatstone bridge is very similar to that of the potentiometer. Wheatstone bridge can only measure low and medium resistance. An ammeter is used to measure high resistances. An ammeter beats the Wheatstone bridge in the category of sensitivity. Let’s learn more about the Wheatstone bridge working principle.
The Wheatstone bridge principle
The Wheatstone bridge working principle is null deflection. The condition of null deflection is the ratio of the known resistances should be equal and that no current should flow through it, i.e., no deflection in the galvanometer. Before working on it, we have to prepare the Wheatstone bridge. In normal conditions, it remains in an unbalanced form. This means current flows through the galvanometer. Only after adjusting the known resistance and the variable resistance can we say that no current flows through the galvanometer. This is called a balanced form.
Diagram of Wheatstone bridge.
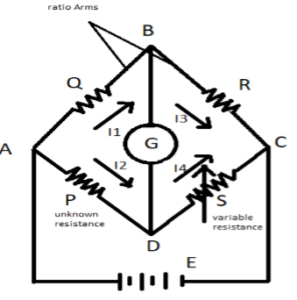
The above diagram is the representation of a Wheatstone bridge. This is the main circuit of the Wheatstone bridge.
- It consists of 4 arms. Each arm has its resistance.
- The resistance R and Q are known. The arms on which they are on are called ratio arms. (AB and BC)
- The resistance P is on the arm AD and is the unknown resistance.
- The resistance S is on the arm DC and is the variable resistance.
- There is a galvanometer G between the AC and BD. This is the source of the null detector.
- E is the battery or the emf source.
The mechanism of the Wheatstone bridge
A potential difference is applied across AC when the Wheatstone bridge is unbalanced and current flows through the galvanometer. The resistance Q, R and S must be varied to achieve a balanced state. The potential difference across AB should equal the potential difference across AD. Then no current will pass, and the galvanometer will show zero deflection. The flow of current is marked in the diagram. Let us find the unknown current P.
Underbalanced conditions, the potential difference across AB is equal to that of AD.
[ as V=IR] Let’s take this as equation (i).
Now when the Wheatstone bridge is balanced, we can also write:
I1 = I3 = E/Q+R and,
I2 = I4 = E/P+S
Now, equating the value of I1 and I2 in equation (i).
E/(Q+R)x Q = E/(P+S) x P
Or, Q/Q+R = 1/(P+S/P)
Or, S/P = (Q+R-Q)/Q
Or, S/P = R/Q
Or, P = QS/R
Here,
- P= unknown resistance
- Q and R= known resistance
- S= variable resistance
Sensitivity
Any movement of a small current can show deflection in the galvanometer. Therefore, the deflection of the galvanometer depends on the sensitivity of the Wheatstone bridge. The formula of sensitivity S is given by:
S= Θ/Ig
This formula is used when we measure current.
S=Θ/Vg
This formula is used when we measure the voltage of the galvanometer.
Here,
- Θ represents the deflection in the galvanometer.
- Ig represents the current that flows through the galvanometer.
- Vg represents the voltage across the galvanometer.
The sensitivity can also be measured as the ratio of the deflection of the galvanometer to the unit unknown resistance.
S= Θ / (△R/R)
Limitations of the device
- Heat is dissipated when current flows through the resistors. Unfortunately, this dissipation of heat changes the resistance of the arms of the Wheatstone bridge. This change can be detected and measured by noting the resistance before passing a current through the resistors. Then, we can properly restrict the current and keep minimum heat dissipation.
- We face a problem when measuring very low resistance on the Wheatstone bridge. We get errors because the resistances of the load and contact become more significant. To mitigate this, the Kelvin double bridge was introduced.
- In case of measurement of high resistances, the Wheatstone bridge fails again. The galvanometer becomes incapable of showing the imbalances. This happens as the resistances become very high and the galvanometer becomes insensitive to the imbalance conditions. We can use a Vacuum Tube Voltmeter in place of the galvanometer and a power supply in place of the battery source. This could avoid the problem.
Conclusion
Kirchoff’s law can also demonstrate the Wheatstone bridge. There are many uses of the Wheatstone bridge. Let us summarise the main points. The diagram of the Wheatstone bridge is very important. One should practice the labels and mark the direction of the arrows. One wrong direction of an arrow can dismiss the whole diagram. The Wheatstone bridge working principle is important. Sums should come from the formula of the unknown resistance and the sensitivity of the Wheatstone bridge. We should also study the limitations of the Wheatstone bridge. One should also go through Kirchoff’s law to better understand the topic.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




