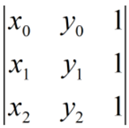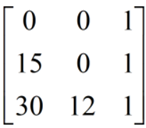Area of triangles using determinants

In this blog post, we will be discussing how to find the area of a triangle using determinants. We will be providing a step-by-step guide on how to do so, as well as providing a diagrammatic representation of statistical data. We hope that you find this information helpful!

How To Find the Area Of a Triangle?

Let’s look at how to find the area of a triangle. While you might think that you’ll need to calculate the area of several triangles, you’ll likely find that it’s much easier than that.

In this section, we will be giving a step-by-step guide on how to find the area of a triangle using determinants. Let’s get started!

Step One: Find out if you have two sides and one angle or three angles. If you do not know what your values are yet, then skip over to step two.

Step Two: Find the area of the triangle using determinants and your values from Step One. If you have three angles, then you will need to subtract them all together before finding out if they are congruent or not.

If there is one angle that needs to be subtracted, then it will be included in the first determinants equation.

Step Three: Find out if your sides are congruent by following these steps below:

1. a) If all three angles of your triangle are congruent, then you can find out straight away that there is no area inside it because angles don’t have an interior.
2. b) If only two angles are congruent, then the third angle will be the one that needs to be subtracted from each of them to obtain an exact answer for what your total surface space is inside a triangular shape with these measurements on its edges.

Area Of Triangles Using Determinants

To find the area of triangles using determinants, we first need to understand what a determinant is. Determinants are used to solve systems of equations, find the area of a triangle, and in many other applications. In the below section we will focus on the last application, finding the area of a triangle.

A determinant is a mathematical function that is used to calculate the size of a particular matrix. In terms of triangles, the determinant can be used to determine the area of the triangle by taking into account the lengths of all three sides.

To calculate the area of a triangle using determinants, we will need to use the following formula:

det =|A|*|b|*|sin(C)|

Where A is the first row of the matrix, b is the second column of the matrix, and C is the angle between the two vectors.

How To Find Area Of Triangle Using Determinants?

Generally, we can find the area of a triangular using Heron’s formula. This is accurate as long as we know the side lengths. Sometimes, we are only given all three vertices, and in these cases, we can find the area of the triangle using determinants.

Once we have the coordinates of all three vertices, we can use determinants to find the area.

First, we will create a matrix using the x and y values of each vertex. Then, we will take the determinant of this matrix. Finally, we will divide that value by two to get our final answer for the area. Let the area of a triangle with vertices at (x0, y0), (x1, y1), and (x2, y2) be A. The corresponding augmented matrix for the triangle will be as follows.

So, the area of the triangle will be:

A=½ [ x0 ( y1 – y2 ) + x1 ( y2 – y0 ) + x2 ( y0 – y1 ) ]

For the sake of this example, let’s say that our triangle has the following coordinates: (0, 0), (15, 0), and (30, 12).

We will create a matrix using those coordinates. The first column will be x values, the second column will be y values and the third column will have 1 at all positions. So our matrix will look like this:

Now that we have our matrix, we will take the determinant of it. The determinant is a calculation that uses all of the values in a matrix and results in a single number. For this calculation, we will use the formula: 

det =  [ x0 ( y1 – y2 ) + x1 ( y2 – y0 ) + x2 ( y0 – y1 ) ].

Plugging in our coordinates, we get the following determinant:

det =0(0-0)+15(12-0)+30(0-0)

= (15*12) + (30*0) 

= 180 + 0 

= 180

Since the determinant is 180, that means that our triangle has an area of 90.

Conclusion

To conclude,  we have shown that the area of a triangle can be found using determinants. We started with a matrix and took the determinant of it to find the area. If the determinant is zero, then the triangle has an area of zero.