Profile
Settings
Refer your friends
Sign out
Calculator of MOI of a rectangular section where the axis of rotation is edge CD of the figure
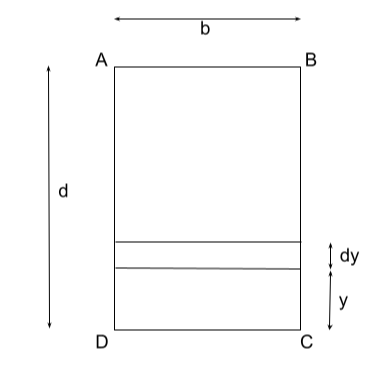
Consider a rectangular cross-section having ABCD as its vertices. Where b is the width of the section and d is the depth of the section. Consider the line or the edge CD as the axis of rotation for this section. Now, let us find the MOI about this line or the axis of rotation CD.
Also, consider a small strip of width ‘dy’ in the rectangular section which is at a distance of value y from the axis of rotation. Involvement of this ‘dy’ will make the assumptions and calculations easier. And after finding the moment of inertia of the small strip of the rectangle we’ll find the moment of inertia by integrating the MOI of the small rectangle section having boundaries from D to A.
Now,
If we see the area of a small rectangular strip having width ‘dy’ will be
dA=dy × b
Consider a rectangular cross-section having ABCD as its vertices. Where b is the width of the section and d is the depth of the section. Consider the line or the edge CD as the axis of rotation for this section. Now, let us find the MOI about this line or the axis of rotation CD.
Also, consider a small strip of width ‘dy’ in the rectangular section which is at a distance of value y from the axis of rotation. Involvement of this ‘dy’ will make the assumptions and calculations easier. And after finding the moment of inertia of the small strip of the rectangle we’ll find the moment of inertia by integrating the MOI of the small rectangle section having boundaries from D to A.
Now,
If we see the area of a small rectangular strip having width ‘dy’ will be
dA=dy × b
Or
dA=bdy
And the moment of inertia of this small area dA about the axis of rotation CD according to a simple moment of inertial formula which is
I=Mr²
Will be
IdA=bdy × y²
Or
IdA=by²dy
Now,
Similar to mathematical derivations, as we found the MOI for the small rectangular strip ‘dy’ we’ll now integrate it to find the same for the whole rectangular section about the axis of rotation CD.
Therefore, the equation or moment of inertia of a rectangular section having a cross-section at its lower edge as in the figure above will be,
ICD=bd³ ⁄ 3
Let us see when we change the axis of rotation, and then how the calculation for the formula changes for it.
Formula when the axis is passing through the centroid
When the axis of rotation of a rectangle is passing through its centroid. The formula for finding the MOI of the rectangle is
I=bd³ ⁄ 12
Where,
b = width of the rectangle and
d = depth or length of the rectangle
Formula when the axis is passing through the base of the rectangle
When the axis is passing through the base of the rectangle the formula for finding the MOI is,
I=bd³ ⁄ 3
Where,
The variables are the same as above, b is the width of the rectangle and d is the depth of it.
Formula when the axis is passing through the centroid perpendicular to the base of the rectangle
In this case, the formula for the moment of inertia is given as,
I=hb³ ⁄ 12
Where,
h is the depth and b is the base of the rectangle.
Conclusion
To sum up, the formula for finding the moment of inertia of a rectangle is given by I=bd³ ⁄ 3, when the axis of rotation is at the base of the rectangle. However, when we change the location of the axis of rotation the formula as well as the value of the moment of inertia of a rectangle changes with it. There are two different methods for finding the moment of inertia of any object, that is, the parallel axis theorem and the other one is the perpendicular axis theorem.
Also see:
