Profile
Settings
Refer your friends
Sign out
Moment Of Inertia is the inherent quality of any object that signifies its tendency not to initiate any angular acceleration, or we can say oppose the rotational inertia if it is present at rest.
Whenever the word, moment of inertia comes, you should understand immediately that there is one object that is either in a rotational motion around a fixed rotatory axis or an object is at a pure rest state, and it is forced to get into a rotational motion.
Just like Newton said in one of his laws of motion, “An object will only change its state of action if there is an external force applied to it.” Similar is the case of inertia in rotational motion. Inertia to avoid modification in an object’s actual state of action is called the Moment Of Inertia. In this article, we have jotted down how to calculate the moment of inertia of a rectangular plate, and moment of inertia of a rectangular plate about its center, and moment of inertia of a rectangular plate about its edge.
Moment Of Inertia Of A Rectangular Plate
Case 1. Moment of inertia of a rectangular plate about its center
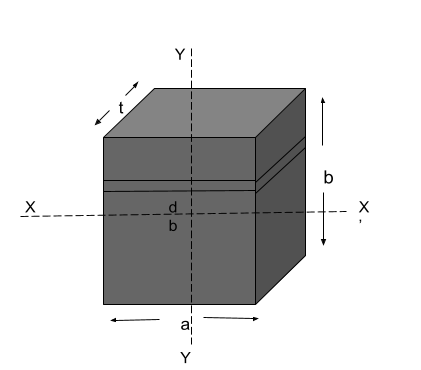
A rectangular plate has a thickness of “t”, length is “a”, and breadth is “b”.
We have to calculate its moment of inertia of the rectangular plate along XX’ axis.
To make our task easy we will consider an elementary infinitely small strip dy and is placed at a distance y from XX’ axis.
Mass of the rectangular plate = Density of body * Volume of body
The density of the material is ⍴.
Therefore, the mass of the rectangular plate = ⍴ * abt.
Mass of the elementary strip = dm = ⍴ * atdyMass moment of inertia for the elementary strip = dI = dmy²
Mass moment of inertia for the rectangular plate as a whole = IXX’ = ∫dI
IXX = ∫dm*y² = ∫⍴ * atdy*y² = ⍴at∫-y²dy = ⍴at[y³/3]
Integrating these equations from -b/2 to b/2.
IXX = ⍴at/3 [b³/8 + b³/8]
IXX = ⍴at*b³/12 = mb²/12Hence, the moment of inertia of a rectangular plate about a line parallel to an edge and passing through the center is mb²/12.
I = {Mass of the rectangular plate * (Width of the plate)²}/12
Case 2. Moment of inertia of a rectangular plate about its edge
A rectangular plate has a thickness of “t”, length is “a”, and breadth is “b”.
We have to calculate its moment of inertia of the rectangular plate along XX’ axis.
To make our task easy we will consider an elementary infinitely small strip dy and is placed at a distance y from XX’ axis.
Mass of the rectangular plate, m = ρ * adt
Mass of the elementary strip out of the plate, dm =ρ * atdy
We will calculate the mass moment of inertia for the elementary plate strip about the x-axis because this axis is passing through one of the edges of this rectangular plate. And, the measurement of the moment of inertia through the x-axis will have the same procedure as calculated from the y-axis or z-axis.
dI = dmy²
Mass moment of inertia for the whole rectangular plate or lamina IX-axis = ∫dI
IX-axis = ∫dm*y² = ∫⍴ * atdy*y² = ⍴at∫-y²dy = ⍴at[y³/3]
Now, comes the difference in approaches from calculating the mass moment of a rectangular plate about a line parallel to the edge that is passing through the center, and the procedure involved in calculating the mass moment of inertia of a rectangular plate when the axis of rotation is passing along one of the three types of edges.
The width of the edge is b.
Therefore, we will integrate the derivative of the mass moment of inertia for calculating the mass moment from one edge. The limits will play the defining role because in the above example the limits were ranging from -b/2 to b/2. But here, the limits will go from 0 to b, because the elementary part has to cover the whole breadth from the x-axis.
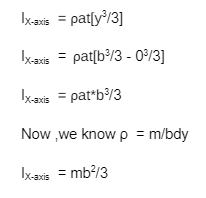
Hence, the moment of inertia of a rectangular plate about a line passing through one of the edges is mb²/3.
I = {mass of the rectangular plate * (width of the plate)²}/3
Conclusion
To sum up, the formula for finding the moment of inertia of a rectangular plate about its center is given by I = mb³/12, when the axis of rotation passes through the center of the rectangular plate and also parallel to the edge. The formula for finding the moment of inertia of a rectangular plate about its edge is given by I = mb²/3. However, when we change the location of the axis of rotation the formula as well as the magnitude of the moment of inertia of a rectangular plate about its center changes with it. We got you the derivations of how to calculate the moment of inertia of a rectangular plate, along with the derivation of moment of inertia of a rectangular plate about its center, and moment of inertia of a rectangular plate about its edge as well.
Important pages
| UPSC Question paper 2022 | UPSC Question paper 2020 |
| UPSC Question paper 2019 | UPSC Syllabus pdf download |
