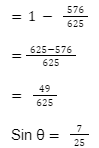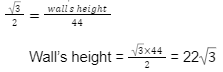Profile
Settings
Refer your friends
Sign out
Sin Theta Formula
Apart from cos and tan, the sine function is an essential trigonometric function.
The ratio of the opposite side and the hypotenuse is known as sine theta. Consider the below right-angled triangle ABC,
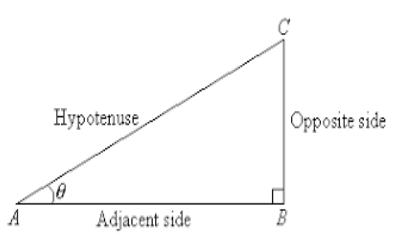
Sin θ = opposite side/hypotenuse = CB/AC
If theta is shifted to C from A, then the formula would transform as below
Sin θ = opposite side/hypotenuse = AB/AC
SIN θ Values
The below table shows the values of sin θ for various degrees
| Sin θ degree | value |
| 0 | 0 |
| 30 | ½ |
| 45 | 1√2 |
| 60 | 3√2 |
| 90 | 1 |
| 180 | 0 |
Sine Wave
The below graph shows how sine wave looks like
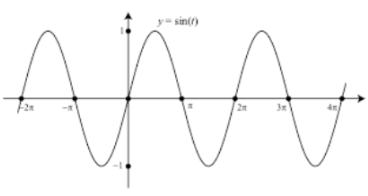
If we look into calculus the differentiation of sin θ = cos θ whereas on integrating we get – cos θ
More Sin Theta Formula
- Sin (- D) = – sin D
- Sin (90 – R) = cos R
- Sin (180 – B) = sin B
- sin2 M + cos2 M = 1
- A+B =Sin A ×Cos B+Cos A ×Sin B
- A-B =Sin A ×Cos B-Cos A ×Sin B
- Sin 2 θ = 2 sin θ. cos θ
- Sin 3 θ = 3 sin θ – 4 sin3 θ
Solved Examples
1. If cos θ = 24/25 then find the value of sin θ using sin theta formula.
We know that, sin² θ + cos² θ = 1
Sin²θ=1- cos²
2. On a building site, John was working. He’s trying to get to the top of the wall. A 44-foot ladder connects the top of the wall to a location on the ground. The ladder forms a 60-degree angle with the ground. What would the wall’s height be?
We know that sin 60 = √3/2, also sin θ here in this case would be wall’s height/ladder
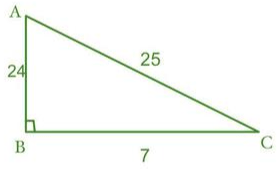
3. In a 7,24,25 right angled triangle at B. what would be the value of Sin C ?
Sin C = Opposite side/hypotenuse
= AB/AC
=24/25
4. In a right angled triangle △ABC at B, if CosA=1/2 then find the value of SinC?
Since the given triangle is a right-angled triangle, and we know that cos 60 = ½ then angle C will measure 30 as per the definition of triangles.
Well then sin 30 = ½
