Profile
Settings
Refer your friends
Sign out
Radius Formula
The length of the line segments that expand outward from the centre toward the perimeter of the figure is sometimes referred to as the radius in more modern use.
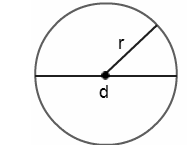
A radius may be any of the line segments that stretch outward from the centre toward the periphery of the figure.
The word “radius” originates from the Latin word “radius,” which may signify both “ray” and “the spoke of a chariot wheel.” R or r is the common shorthand and term given to the mathematical variable that represents the radius. By analogy, the diameter, denoted by the letter D, is equal to two times the value of the radius.
The formula for the radius may be easily calculated by dividing the diameter of the circle in half. When a point on the ring’s perimeter is connected to the very centre of the circle, the resulting line segment is referred to as the ring’s radius.
The radius is defined as the distance that is measured outward from the centre of the circle toward its perimeter. Always diameter is twice as big as the radius. The formula may be obtained by first dividing the diameter by 2, as shown.
Radius formula in terms of diameter, circumference, and area are-
r= d/2
r= C/2π
r= √(A/π)
Here,
r is radius
C is circumference
A is area and,
d is the diameter.
Solved Examples
1. Find the radius of the circle whose diameter is 50cm.
Given,
Diameter = d = 50 cm
Radius = (d ⁄ 2) = 50 ⁄ 2 cm = 25 cm
2. Find the radius of the circle whose diameter is 19cm.
Given,
Diameter = d = 19 cm
Radius = (d ⁄ 2) = 19 ⁄ 2 cm = 9.5 cm
3. Find the radius of the circle whose diameter is 80cm.
Given,
Diameter = d = 80 cm
Radius = (d ⁄ 2) = 80 ⁄ 2 cm = 40 cm
