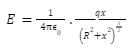Concept of Gauss Law

According to Gauss Law, the charge enclosed divided by the permittivity equals the total electric flux out of a closed surface. The electric flux in a given area is calculated by multiplying the electric field by the area of the surface projected in a plane parallel to the field.

Gauss Law:-

The total flux associated with a closed surface equals 1/ε0 times the charge encompassed by the closed surface, according to the Gauss law.

 i.e.,∮{E.ds}=1/ε0q

A point charge q, for example, is placed within a cube with edge ‘a’. The flux through each face of the cube is now q/6ε0, according to Gauss’ law.

The electric field is the most fundamental idea in understanding electricity. In general, the electric field of a surface is computed using Coulomb’s equation, however understanding the notion of Gauss law is required to calculate the electric field distribution in a closed surface. It explains how an electric charge is enclosed in a closed surface or how an electric charge is present in a closed surface that is enclosed.

Formula of Gauss Law:-

According to the Gauss law, the total charge contained within a closed surface is proportional to the total flux contained within the surface. As a result, the total electric charge Q encompassed by the surface is; if Φ is total flux and ε0 is electric constant

 i.e.,Q = Φ ϵ0

The Gauss law formula is as follows:

Φ = Q/ϵ0

Where,

Q = total charge in the given surface,

 ϵ0 = the electric constant.

Some more clarification about this law:-

The net charge in the volume enclosed by a closed surface determines the net flow through the closed surface.

The Gauss theorem is a relationship between the ‘flow’ of electric field lines (flux) and the charges within the enclosed surface. The net electric flow stays zero if no charges are encapsulated by the surface. This signifies that the number of electric field lines entering and leaving the surface is equal.

A significant corollary of the Gauss theorem is:

The only sources (positive charges) and sinks (negative charges) of electric fields confined by the surface account for the electric flux from any closed surface. The electric flow is unaffected by any charges that exist outside the surface. Furthermore, only electric charges can serve as electric field sources or sinks. For example, magnetic fields that change cannot operate as electric field sources or sinks.

Because it encloses a net charge, the net flow for the surface on the left is non-zero. Because the right-hand surface does not encapsulate any charge, the net flux is zero.

Application of Gauss Law:-

1. In the case of a charged ring of radius R rotating on its axis at a distance x from its center.                              X = 0 and E = 0 are at the center.

2. At a distance of ‘r’ from an infinite charge line 

Where  λ is the linear charge density.

3. E =20K ,where σ is the surface charge density, is the intensity of the electric field near a plane sheet of charge.

4. In a medium with a dielectric constant of K, the intensity of the electric field near a plane charged conductor E = σ/Kε0. When air is used as the dielectric medium, Eair = σ/ε0.

5. Where σ is the surface charge density, E = σ/ε0 is the field between two parallel plates of a condenser.

Conclusion:-

Gauss’s law, often known as Gauss’s flux theorem (or just Gauss’s theorem) in electromagnetic theory, is a law that relates the distribution of electric charge to the resulting electric field. It asserts that the flux of the electric field out of any closed surface is proportional to the electric charge enclosed by the surface, regardless of how that charge is distributed, in its integral form.