Cells, often known as electrochemical cells, are devices that generate electricity. The chemical reactions that take place within these cells provide the energy. Cells, often known as batteries, are a common day-to-day product that are required for a variety of functions.
It’s crucial to remember that a battery is made up of cells. It also behaves differently when used in different circuits (in series or parallel). The mathematical equations for linking cells in series and parallel, as well as a set of solved cases based on them, are presented in this article.
Cells
A cell is a device that generates electricity from chemical energy and maintains the passage of charge in a circuit.
Electrodes and electrolytes make up a cell. As conductors, the electrodes transmit current via the circuit. The anode, or positive terminal of the cell, is the electrode with the higher potential. The cathode, or negative terminal of the cell, is the electrode with the lowest potential.
When a cell is connected to an external load, it produces energy. Outside the cell, current flows from anode to cathode, but inside the cell, current flows from cathode to anode.
EMF
When there is no current in the cell or the cell is in an open circuit, the electromotive force (EMF) is defined as the potential difference between the positive and negative electrodes. The EMF of the cell initiates the passage of current in the cell.
Volts is the SI unit of EMF (V). EMF’s formula is as follows:
ϵ=E/Q
Here,
= EMF in volts
E= Energy in joules
Q= Charge in coulombs.
The EMF can be re-written as:
ϵ=IR+Ir
Here,
ϵ= EMF in volts
I = Current in Ampere
R is load resistance in ohms,
r is the internal resistance of a cell in ohms.
Internal Energy
When current flows through a circuit, internal resistance is defined as the resistance given by the electrolyte and electrodes. The electrolytes and electrodes work against the current flow. The letter ‘r’ stands for internal resistance.
Consider a cell with two electrolytes connected by an external resistance, indicated by the letter ‘R.’ From cathode to anode, current will flow.
Closed Circuit: V=V1+V2-Ir
Where (V1+V2) = Initial potential difference,
Cells in Series
There are two main types of cell connections: series and parallel. Cells can be linked in series, parallel, or a hybrid of the two.
Electrons in a series circuit can only go in one direction. The current flowing through each resistor will be the same in this case. In a series connection, however, the voltage across each resistor will be different. As a result, circuits connected in series are much less likely to overheat.
Electrons in a parallel circuit travel through multiple branches. In a parallel circuit, the voltage across each resistor in the circuit remains constant, and the cells can be arranged in any way.
A series is formed when many cells are organized in such a way that the positive terminal of the first cell is connected to the negative terminal of the next cell, and this pattern continues. This arrangement is referred to as a series combination.
The following is a diagram of the arrangement:
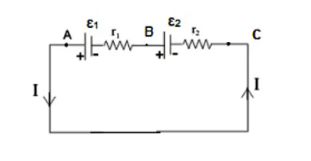
Let us Consider the EMF of the first cell is = ε1 and the EMF of the second cell is = ε2.
Consider there are 3 points A, B and C as shown in the figure. Here the potential at point A= VA and the potential at point B=VB and the potential at point C=VC.
Let us consider that the circuit is closed. As a result, there will be some flow of current. In this case Resistance will be offered by the cell itself.
Generally the Internal resistance of first cell =r1 and Internal resistance of second cell is=r2.
For an open Circuit
Potential difference between points A and B (VA-VB)= Potential difference between the 2 electrodes.
Hence, VA-VB=€1-Ir1…eq(1)
Where, Ir1= Voltage drop across the internal resistance.
Similarly for equation for Potential difference E2:
VB-Vc=€2-Ir2…eq(2)
Now, Adding (1) and (2) we get:
VA-VC=1-Ir1+2-Ir2
VA-Vc=€1+€2-Ir1+r2…eq(3)
Consider there are only 2 cells then EMF = €equivalent=(€1+€2 )
and Resistance = requivalent=(r1+r2)
Now using equation 3 we get
VA-VC=equivalent-Irequivalent…eq(4)
Now, comparing RHS of equation (3) and equation (4):
€equivalent=(€1+€2) and requivalent=(r1+r2)
For cells arranged in series
The equivalent EMF is the total of the individual EMFs. The equivalent resistance is the sum of the individual resistances.
Let us consider n to be the number of cells that are connected in series and connected across an external resistance R.
Let Internal resistance of each cell =r, EMF =ε
Total resistance = R +requivalent
Where R=external resistance of the external circuit.
Total resistance = R + nr where nr is the sum of all the n resistances.
Thus the effective EMF of cells = nε, where nε (EMF of each cell).
Therefore current flowing through resistance is equals to:
I=Effective EMF/Total Resistance=nE/R+nr
Conclusion
In this article we have studied about cells and about series connection of cells. A cell is a device that generates electricity from chemical energy and maintains the passage of charge in a circuit.
Electrodes and electrolytes make up a cell. As conductors, the electrodes transmit current via the circuit. The anode, or positive terminal of the cell, is the electrode with the higher potential. The cathode, or negative terminal of the cell, is the electrode with the lowest potential.
A series is formed when many cells are organized in such a way that the positive terminal of the first cell is connected to the negative terminal of the next cell, and this pattern continues. This arrangement is referred to as a series combination.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






