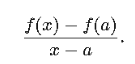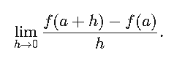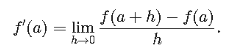Definition of Derivatives
Derivatives are simply a measure of the rate of change of a variable with respect to other variables. It can be the rate of distance change concerning time or the temperature concerning distance. We want to measure the rate of change of a function y = f ( x ) with respect to its variable x.
The first principle of differentiation helps us evaluate the derivative of a function using limits. Calculating the result of a process using the first principle of differentiation may be a tedious task. We may employ identities and tricks to calculate the limits and evaluate the required derivative.
The first principle of derivatives is nothing, but it is the function’s first derivative. We have the first derivative of position with the limit of zero. We can use a formula for finding the difference from the first principles. Product by the first principle refers to using algebra to find a general expression for the slope of a curve. It is also known as the delta method.
Examples of Derivative
While filling a bucket with water from the tap, we need to know the flow of water from the tap to determine when the bucket will be served. Thus, the water flow rate is the derivative function we consider. Thus a derivative of operations is the rate of change of a value at a point.
A prevalent and easy-to-understand example of a derivative is the slope of a line. We know that the slope of a line can be calculated in many ways. It is also equal to the tangent of the angle of the line with the x-axis. The slope of a line is the rate of change of the value of points on the curve.
Formula for First principle of Derivatives:
f ′ ( x ) = lim h → 0 (f ( x + h ) − f ( x )) /h
Derivative by the first principle refers to using algebra to find a general expression for the slope of a curve. It is also known as the delta method. The derivative is a measure of the instantaneous rate of change.
We want to measure the rate of change of a function
y = f(x) with respect to its variable x.
The general notion of rate of change of a quantity y with respect to x is the change in y divided by the change in x, about the point a. This describes the average rate of change and can be expressed as:
To find the instantaneous rate of change, we take the limiting value as x approaches a. To simplify this, we set x=a+h, and we want to take the limiting value as h approaches 0. Thus, we have
If this limit exists and is finite, then we say that:
Wherever the limit exists is defined to be the derivative of f at x. This definition is also called the first principle of derivative.
Some Basic Functions of Derivative:
- If y = ax , where a is a constant, dy/dx = a
- y = xn , where n is an integer, dy/dx = nxn-1
- If y = sinx, dy/dx = cosx
- y = tanx, dy/dx = sec2x
- If y = a ,where ‘a’ is a constant, then dy/dx=0
Solved Examples
Question 1. Differentiate from first principles for the function 3x
Solution. The function given in the question is,
f(x)=3x
To find differentiate from first principle of the above given function by using the formula,
Substitute the function in the formula of first principle we get,
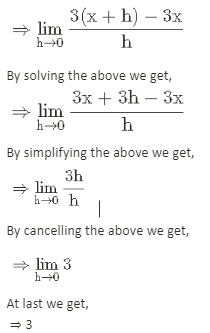
Therefore, The required first derivative of the above given function is 3.
At last if the value of the function has h then we have to substitute the limit value to that. The derivative of any constant will be equal to zero otherwise we can say it as the derivative of any whole number is equal to zero.The derivative of a function y=f(x) is also represented by f’(x).
Question 2. Find f ‘(x) when f(x) = 1/x2
Solution: When f(x) = 1/x2 = x-2, using the above laws
d(xn)/dx = nxn-1
f ‘(x) = -2x-3
f ‘(x) = -2/x3
Derivative’s First Principle
Let y = f(x) ——– (1)
Let Δx be a small change in x such that Δy will be a small change in y.
Therefore, y + Δy = f(x+ Δx) ————-(2)
Now (2) – (1),
y + Δy – y = f(x + Δx) – f(x)
The above equation becomes,
Δy = f(x + Δx) – f(x)
Now dividing both sides by Δx we have,
Δy/Δx = [f(x+ Δx) – f(x)]/Δx
When Δx → 0
We have,
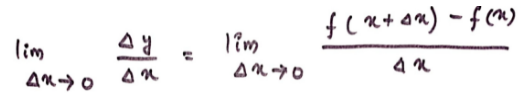
If the limit exists, then it is called the derivative of y with respect to x and will be denoted as dy/dx or df(x)/dx or f′(x).
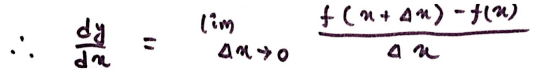
Application:
Derivatives by first principle is often used in cases where limits involving an unknown function are to be determined and sometimes the function itself is to be determined.
Conclusion:
- Tangent at a point (slope) is obtained by simply applying the first derivative principle at that point.
- Slope of a tangent is denoted by (dy/dx).
- Geometrically, finding derivative at a point P (suppose) is equivalent to finding slope of tangent at that point (here P)
[Note: Slope is nothing but a measure of the rate change]
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out