Profile
Settings
Refer your friends
Sign out
A Brief Introduction to Spring Mass Systems
A spring-mass system consists of a spring whose one end is fixed or attached to the rigid support, whereas a block of mass is hung from the other end. The spring-mass system is useful in finding out the time period of any object performing the simple harmonic motion. It is also applicable to a wide variety of real-life applications.Â
Introduction to Two Block Spring SystemÂ
In a two-block spring system, two masses are there. These masses are connected together through a spring. This system is kept on a smooth, frictionless surface. Initially, the blocks are at rest and the spring is unstretched. When an external force is applied to one of the blocks, the system starts moving with some acceleration and the spring is stretched. Our motive is to calculate the extension of the spring.Â
Understanding Two Block Spring System Experiment and Mechanism
Let us perform an experiment for a two-block spring system to calculate the extension of the spring. Let there be two masses whose values are m and M. Let them be connected by a spring whose spring constant is k.Â
A force of F1 is applied to the mass m and a force of F2 is applied to mass M, as a result of which the system starts moving in the opposite direction. Let the mass m is displaced by a distance x1 and the mass M is displaced by x2.Â
The total work done by the forced F1 and of F2 isÂ
Different Arrangements of Spring Mass Systems
Two different arrangements of the spring-mass systems are possible. These are:Â
The parallel combination of the springs:Â
In a parallel combination of the springs, the springs are connected in parallel with the mass. The displacement of each spring is the same, but the restoring forces are different.Â
The equivalent spring constants of a parallel combination are given byÂ
k = k1 + k2 + k3 + … + kn
Series combination of the springs:
In a series combination of the springs, the springs are connected in series with the mass. The displacement of each spring is different, but the restoring forces are the same.
The equivalent spring constants of a series combination are given by
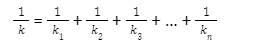
Time Period of a Spring Mass System
The time period is defined as the time required by the spring-mass system to complete one oscillation. Frequency is the opposite of the time period and is defined as the number of oscillations made in one second.Â
                                        T = 1 / f
The time period of a spring-mass system is given by the equation:
T = 2 π (√m/k)
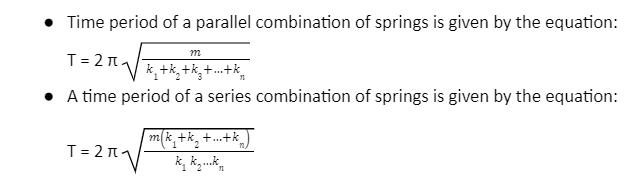
Factors that Affect the Time Period of a Spring Mass System
It is clear from the formula of the time period that the time period of a spring-mass system is directly proportional to the square root of the mass and inversely proportional to the square root of the spring constant of the spring. This means that a heavy object will have more time period as compared to a light object. The time period is free from the gravitational acceleration of the earth and the amplitude. A constant force also does not affect the time period of a simple spring-mass system.Â
What type of motion Does a Spring Mass System have?
The spring-mass system performs simple harmonic motion. This system is an example of a vibrating system. When an external force is applied to the system, it starts vibrating to and fro, depicting a simple harmonic motion. The simple harmonic motion follows Hooke’s Law. This implies that the spring-mass system also obeys Hooke’s Law.
Conclusion
This article explains about the spring-mass system in detail. It explains from scratch about the spring, its combinations and the different types of systems. It also tells about the time period and its dependency. We hope this article proves to be helpful.
