The Value Of Spring Constant

Spring constant

The pressure of spring has calculated the use of Hooke’s law, named for Robert Hooke, the 17th-century British physicist who evolved the formulation in 1660 as he studied springs and elasticity. When pressure is positioned at the cloth, he observed that the cloth stretches or compresses in reaction to the pressure.

Hooke’s law is a physical law that shows that the force (F) required to stretch or compress a spring at a particular distance (x) is linearly proportional to that distance. Fs = kx, where k is the constant coefficient characteristic of the spring (that is, its stiffness), where x is small compared to the total possible deflection of the spring. The law is named after the 17th century English physicist Robert Hooke.

Spring is an elastic machine that returns to its original shape after deformation, that is, expansion or contraction, or compression. These are the components required for various mechanical devices.

Spring force is the force required or applied to compress or expand the spring of an object attached to it. When an object exerts a force on a spring, the spring exerts an equally opposite force on the object. It always acts to return the mass to the equilibrium position. The spring constant is a characteristic of a spring that measures the ratio of the force acting on the spring to the displacement caused by the spring. In other words, it represents the stiffness of the spring and how much it expands and contracts. A spring with a large spring constant will have less deflection than a spring with a smaller spring constant for the same additional mass.

The unit of spring constant

In SI units, displacement is measured in meters (m) and force is measured in Newton (N or kg m / s²). Therefore, each element of the spring constant k and tensor κ is measured in Newton/meter (N / m) or kilogram / square second (kg / s²).

For a continuous medium, each element of the stress tensor σ is the force divided by the area. Therefore, it is measured in the unit of pressure, Pascal (Pa, or N / m², or kg / (ms²). The element of the strain tensor ε is dimensionless (displacement divided by distance), therefore Cijkl. The entry is also expressed in units of pressure.

Formulas of spring constant for linear springs

Consider a simple coil spring with one end attached to a solid object while the free end is being pulled by a force of magnitude Fs. Suppose the spring reaches equilibrium and its length does not change. Let x be the amount by which the free end of the spring is displaced from its “relaxed” position (if not stretched). Then, 

Fs = kx

Or,

x = Fs / k

Where k is a positive real number characteristic of springs, in addition, the same formula applies when the spring is compressed. In this case, both Fs and x are negative. According to this equation, the graph of the force Fs applied as a function of the displacement x is a straight line through the origin, the slope of which is k.

Formulas of spring constant for linear springs

Consider a simple coil spring with one end attached to a solid object while the free end is being pulled by a force of magnitude Fs. Suppose the spring reaches equilibrium and its length does not change. Let x be the amount by which the free end of the spring is displaced from its “relaxed” position (if not stretched). Then, 

Fs = kx

Or,

x = Fs / k

Where k is a positive real number characteristic of springs, in addition, the same formula applies when the spring is compressed. In this case, both Fs and x are negative. According to this equation, the graph of the force Fs applied as a function of the displacement x is a straight line through the origin, the slope of which is k.

Tensional stress of a uniform bar

A rod of elastic material can be thought of as a linear spring. The length of the rod is L and the cross-section is A. Its tensile stress σ is linearly proportional to the breakpoint elongation or elongation ε via the elastic modulus E.

σ = Eε

In many cases, the modulus of elasticity can be considered constant. so,

ε = ∆L / L

(the fractional change in the length) and since, 

σ = F / A

so,

ε = σ / E

= F / AE

We can express the change in the length in the form of 

∆L = εL = FL / AE

Spring energy

The potential energy Uel (x) stored in the spring is given by the following equation:

Uel (x) = ½ kx²

This is the result of adding the energy required to compress the spring in stages. That is, the integral of the force with respect to the displacement. The potential energy of the spring is always non-negative because the external force has the same general direction as the displacement.

When the spring is stretched in the positive x-direction, the potential energy increases parabolic (even if the spring is compressed). Because the potential energy changes are constantly changing:

d² Uel / dx² = k

The change in U change is constant, even when the displacement and acceleration are zero.

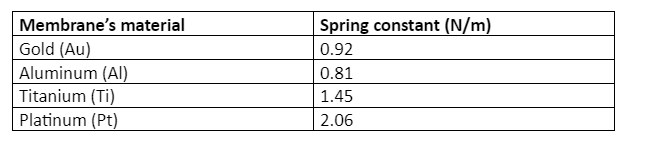
Table of constant spring values