Speed of Sound in a Medium
In longitudinal waves, the medium’s components oscillate in the same direction as the wave’s propagation. The inertial and elastic properties of the medium also influence the speed of a longitudinal wave.
There are compressions and rarefactions of longitudinal waves, such as sound. As a result, the elastic property of a medium may be linked to its bulk modulus.
Bulk modulus B = -ΔP ⁄ ΔV ⁄ V, where
Δ P = Change in pressure
Δ V = Change in volume
V = Initial volume
Further, the inertial property relevant for the propagation of these waves is the mass density( ) of the medium. Speed of longitudinal waves can be deprived easily using dimensionless analysis.
Dimensions of Bulk modulus B = M¹L-¹T-²
Dimensions of mass density = M¹L-³
By simple inspection, we get the formula for the speed of longitudinal waves as

In the case of a linear medium like a solid rod, the relevant modulus of elasticity is Young’s modulus Y. The ratio of tensile (compressive) stress to the corresponding longitudinal strain is called Young’s modulus. Therefore, in the case of solids, the velocity of the longitudinal wave is given by v = √Y ⁄ P.
Effect of density of the medium on the speed of sound
Solids and liquids have a higher sound speed than gases despite their denser nature. This is because of their larger bulk modulus, which makes them more difficult to compress than gases. This makes up for the fact that they are heavier than gases.
Larger molecules would slow down the transmission of sound waves, which are made up of kinetic energy. In order to vibrate a huge molecule, it would require far more energy than a smaller one. The denser item has a lower sound speed because they both share the same elasticity qualities.
Now, let us take up some sample questions.
Q1. The speed of longitudinal mechanical waves in a material is 4200 m/s. Young’s modulus of the material is 15109 N/m². What is the density of the material?
Ans. Using the formula for speed of longitudinal wave,
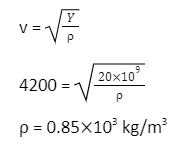
Q2. If the speed of longitudinal mechanical waves in water is 1400 m/s, then calculate the Bulk modulus of elasticity of the water. (Given = Density of water is 1 g/cm³).
Ans. Speed of longitudinal wave v =√ B ⁄ P
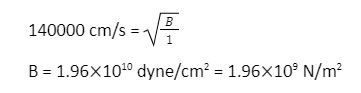
Q3. Calculate the speed of longitudinal waves in steel. Young’s modulus for steel is 31010 N/m², and its density is 1.210³ kg/m³.
Ans. Speed of longitudinal wave v =√ Y ⁄ P
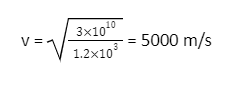
Other factors affecting the speed of sound:
1.Elasticity
Elasticity is the property of the material of a body due to which the body opposes any change in its shape and size when deforming forces are applied to it and recovers its original configuration partially or wholly as soon as the deforming forces are removed.
A material like aluminium would experience small deformation as compared to rubber, in case an equal force would be applied to both. Therefore, the sound would travel at a faster rate in aluminium due to its higher elasticity than rubber, which has a lower elasticity. As a result, the sound waves travel fastest in solids, then liquids and lastly followed by gases.
2.Temperature
With increasing temperature, the density of air decreases. In a warm gas, the molecules acquire higher kinetic energy to travel at a faster rate than the molecules at room temperature and lower than that. Therefore, at a constant volume and a high temperature, more masses of molecules can occupy the same space. Hence, it is inferred that at high temperatures in gases, the speed of sound increases.
Conclusion:
In this article, we saw an overview of the effect of density on the speed of sound. The longitudinal waves, such as sound, travel in the form of compressions and rarefactions. The speed of sound is greater in solids and liquids than in gases because they are much more difficult to compress than gases, and so have much higher values of the bulk modulus. For given two objects, the speed of sound would be slower in the denser object, considering they both have the same properties of elasticity. So, the density of a medium is inversely related to the speed of sound. We also saw other factors like elastic properties and temperature, which affect the speed of sound.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out













