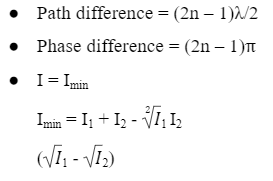Superposition of Waves

An interference wave is a phenomenon in which two or more waves superpose each other at the same time in the same medium. This phenomenon of superposition of waves depends on the arrangements of troughs and peaks of the waves that overlap which may cancel each other totally or to some extent and might add up to one another. The interference wave pattern occurs due to the two coherent and independent waves when they superpose with each other.

The Principle of Superposition of Wave

According to the principle of superposition, when two or more two waves intersect at a point, at that point the displacement is equivalent to the addition of each waves’ displacement. Each wave may be negative or positive. The summation is done by vector addition if the individual displacements are of vectors. Diffraction, standing waves, and inference are explained by the idea of superposition. 

Let us consider, two waves that are traveling with a displacement of 

y1 (x, t) and y2 (x, t). 

When, the two waves intersect the resultant displacement is considered as y (x, t)

Mathematically, this can be written as,

y (x, t) = y1 (x, t) + y2 (x, t)

According to the superposition’s principle, the waves that are intersecting at a point can be summed up algebraically for producing the resultant wave. The moving wave’s wave functions can be assumed as 

y1 = f1 (x – vt)

y2 = f2 (x – vt)

……… yn = fn (x – vt)

The disturbance in the medium described by the wave function can be given as

y = f1 (x – vt) + f2 (x – vt) + …. + fn (x – vt)

• y = i=1 to n = fi (x – vt)

Let, the wave that is moving by the side of a stretched string is

y1 (x, t) = A sin (kx – ωt) 

And let, another wave which has shifted from the first wave by a phase of φ is

y2 (x, t) = A sin (kx – ωt + φ)

In the above two equations, it can be seen that ‘wave 1’ and ‘wave 2’ have similar angular wave vector k, angular frequency is the same for both; therefore, they have an equivalent wavelength and similar amplitude A.

Hence, by applying the principle of superposition, the resultant wave is the summation of the two waves that were taken into consideration

y (x, t) = A sin (kx – ωt) + A sin (kx – ωt + /2)

Constructive and destructive interference

Constructive Interference

Constructive interference is defined as when two respective waves move in a similar direction in a similar phase, the two wave’s amplitude is added and as a result, the resultant wave comes as a consequence of this. This phenomenon of waves is called constructive interference. When the wave goes through constructive interference upward displacement occurs. Therefore, this upward displacement is more than the two interfering pulse’s displacement. When one wave’s crest meets or intersects the other wave’s crest having similar frequencies, then the summation of each wave’s amplitudes is the resultant amplitude. So, it can be observed that the resultant wave’s amplitude is more than the waves that go through interference. When the even multiple of (180°) is the phase difference between the two waves, then constructive interference occurs. A new wave is formed which looks exactly like the original waves but there is a difference between these two waves is that the amplitude of a new wave is larger than the original wave in constructive interference. 

The equations related to destructive interference are –

The phase difference between two waves = n

The path difference between two waves ∆ = nλ

The time interval between two waves ϴ = n T

Destructive interference

Destructive interference of light is defined as when two waves of light come together, they fully cancel one another. In destructive interference, the two waves should have a similar amplitude but they must be in opposite directions. To examine the destructive interference of light the principle of superposition is used which says, when two or more two waves are moving in the same medium, then the resulting wave function is the summation of each wave function. The equations related to destructive interference are –

The phase difference between two waves = (2n – 1)

The path difference between two waves ∆ = (2n – 1) λ/2

The time interval between two waves ϴ = (2n – 1) T/2

Conclusion

It is to be concluded that the superposition of a wave is when two or more than two waves intersect or overlap at a point, for producing a resultant wave, the summation of waves that are intersecting at a point is calculated. There are 2 categories of superposition of interference waves, such as constructive and destructive interference.