Profile
Settings
Refer your friends
Sign out
The term black body radiation might be daunting for a few but do not fret; we shall be describing what it is shortly. For now, we shall just think of Stefan Boltzman as a theory that describes how different bodies emit radiation or conversely, a law that allows us to calculate the temperature of a body from the power or energy that it radiates. This has the most important applications in astronomy, as we’ll discuss later in the article.
The Stefan-Boltzman Law
The Stefan-Boltzman law was first put forward empirically by Joseph Stefan in 1879, drawing upon the work from John Tyndall’s experimental measures in 1864 and later given a theoretical derivation by Ludwig-Boltzmann in 1884. Boltzmann initially presented his work from the viewpoint of thermodynamics. Alternatively, a derivation can also be taken from Plank’s law which was put forward in 1900 as a solution to the ultraviolet catastrophe. Those who wish to know what that is is highly encouraged to look up the topic as it is one of the most important stepping stones to the foundation of one of physics’ most successful theories, Quantum mechanics.
Now we’ll get to the juicy part of the theory, namely the equation first put forward by Stefan.
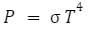
Where is the Stefan-Boltzmann is constant
The theory as described now would represent the radiation due to a black body. Now, what is a black body? A black body is an idealized body created by physicists to describe radiating bodies. A black body is a physical body which absorbs all radiation that falls on it. Such a body does not exist in real life as anybody that absorbs radiation would also reflect a part of the radiation that falls on it.
Now, as the black body absorbs incoming radiation, it gets heated and the heat is re-emitted in the form of radiation. The Stefan Boltzmann law describes this emitted radiation. Now to generalize this for normal everyday bodies, we introduce another factor called emissivity (e).
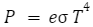
Where e can take any value between 0 and 1, with e =1 representing a black body.
The emissivity can be understood by looking at what happens to any radiation that falls on a given body; some radiation gets absorbed, some gets reflected and some passes through the body. Now, if t is the fraction transmitted, r is the fraction reflected and a is the fraction absorbed, we can write –
A+r+t = 1
Now any good absorber is a good emitter. Thus, we will take e(emissivity) to equal the absorbance(a) in most practical cases.
We’ll now look at how the law can be derived and then explain a couple of its applications to get the reader to understand the usage of this theory properly. We shall be describing the derivation of Stefan Boltzman’s equation law from Planck’s law.
Planck’s law can be written as –
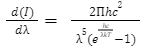
Where I is the power radiated per unit area. On integrating this equation over all possible wavelengths from 0 to infinity to account for energy from the whole of the spectrum, we shall get an equation of the form –
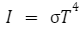
Where is a constant made up of the different h, c and k factors. The reader is encouraged to manually try this integration and find out what the constant is exactly. The value of the constant on calculation comes out to be 5.67 x 10^8. On changing I into P/A and inserting it into the equation, we’ll get back to the regular equation –
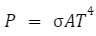
This is the simplistic derivation based on Planck’s law. The reader is also encouraged to go through the initial theoretical derivation presented by Boltzman to understand the law better.
Now to acquaint the reader with the applications of Stefan’s law, we shall demonstrate one of its earliest and most popular applications in astronomy, calculating the radius of the stars.
From Stefan Boltzman’s law, we shall first rearrange the equation to be able to find the temperature. We shall consider e =1, that is, we consider the star to be an ideal emitter of radiation.
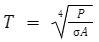
The temperature can be calculated from spectrum studies and thus knowing the temperature and intensity, one can calculate the area, which in turn gives us the radius of stars.
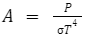
Conclusion
From the article given above, we can conclude that it is an indispensable tool in thermodynamics, the study of heat and its relationship to other types of energy. Hence it is used in various theories and thesis. It is used to solve the problem based on wavelength and radiation.
