Profile
Settings
Refer your friends
Sign out
A rigid entity’s MOI or the moment of inertia, also known as its mass moment of inertia or resistivity towards angular momentum is a measure that stipulates the force needed by an axis of rotation for a preferred rotational motion, similar to how mass determines the energy exerted for such preferred acceleration.
Speaking about the moment of inertia of a rigid or solid cone, it is an unsymmetrical body or object which is derived using a small piece of disk taken inside that and finding the moment of inertia of that particular small piece and at last integrating the moment of inertia of the small disc to the extent of the cone to find out the moment of inertia of the complete solid cone.
For an instance, the moment of inertia of a solid cone is given by the equation
I=3MR² ⁄ 10
Where,
M = mass of the solid cone
R = distance from the axis of rotation or radius from the axis of rotation
I = Moment of inertia of the solid cone
In this article, we would have a look at how we can derive the above formula using the same method as written in paragraph 2 of this article.
Derivation
Before deriving the equation let us discuss the assumptions needed for it and a diagram representing our cone and the small disc with their attributes.
So, consider a cone having its axes as X, Y and Z. While the cone is standing vertically on the Z-axis. The radius of the complete cone is determined by the attribute R and the radius of the small disc inside the cone is denoted by the attribute r. And having the z-axis as the axis of rotation. The height of the cone is determined by the attribute h and the thickness of the disc is denoted by the attribute dz.
Taking the mass of the small disc as equation,
Here, equation 3 denotes the small mass of the small elemental disc which will be used in the coming equations. As we know for finding the moment of inertia we should know the mass of the object or the small particle as well as the distance from the axis of rotation. Therefore, we found the same in equation 3.
Now,
Considering the moment of inertia of the disc about the z-axis, will be equationed as,
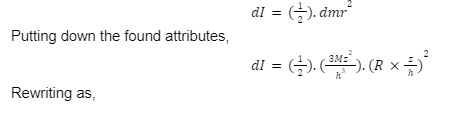
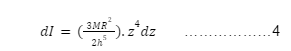
Equation 4 above denotes the moment of inertia of the small elemental disc we assumed inside the cone. Now as we said, we’re gonna integrate the equation to find out the complete moment of inertia of the whole solid cone. So, here we go,
Integrating equation 4 with limits having from 0 value in the z-axis to the height of the cone.
Conclusion
A cone is a symmetrical object or entity, and the formula for finding the moment of inertia of this kind of entity about an axis passing through the centre of the cone and perpendicular to it is done by taking a small elemental disc inside it and finding the moment of inertia of that particualr disc by common formula, which is the product of the mass of the element and the square of the distance between the element and the axis of rotation. And after finding that we need to integrate the moment of inertia of that small elemental disc having limits as the height of the cone to find out the complete solid cone moment of inertia.
