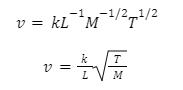The relation among physical quantities can be deduced by the application of Dimensional analysis. For this we need to know dependency and other related concepts with the help of an example. For example, suppose we want to move a box from one point A to the other point B. For this, we need to apply some force on the box to make it reach the destination point. The factors that will help in determining the extent of force (say F) will be the weight of the box (say M), Distance from point A to point B (say L), and time to be taken to move the box (say T). Hence we can say that Force is the function of its mass, distance or length, and time taken. This can be numerically expressed as:
F=fM,L,T
Now, we will learn how to derive an exact formula to do that.
![]() Concepts Used
Concepts Used
Followings concepts are applied for deducing the relation among physical quantities:-
Units of Measurements:- Units are the numerical measures in which the result of the measurement of a physical quantity is expressed.
Physical Quantities:- The quantities which can be measured by an instrument and which describes the laws of the physical world. Fundamental physical quantities are the ones that do not depend on any other physical quantity. (Example: Length, mass, time, etc.)
Dimensions of physical quantities:- Dimensions are the powers (or exponents, or indices) to which the fundamental units of physical quantities are raised.
Dimensional Analysis: Principle of Homogeneity:- The dimensions of each term of an equation must be the same. In other words, we can make addition or subtraction of similar physical quantities. The above-mentioned statement that we can make addition or subtraction as per the requirement in order to make dimensions of each term of an equation the same is used as an analysis known as dimensional analysis.
Steps For Creating An Equation
Following are the steps to be followed to form an equation for deducing relation among the physical quantities:-
Consider powers for each physical quantity (say a,b,c,…so on).
Write the dimensional formula on both sides.
Compare the powers to get their values.
Put the values of powers obtained in the above equation.
Simplify it to get the required equation.
Deducing Relation Among Physical Quantities: Examples
Example 1: Deriving expression for the time period of oscillation of a simple pendulum.
Time T is the function of mass of the bob M, its length L, and gravity g which can be numerically expressed as:
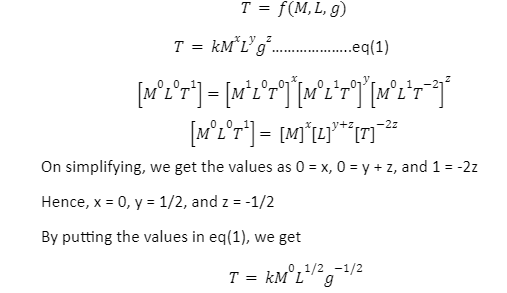
This is the numerically expressed relationship among the period of time, mass, length, and gravity.
Example 2: Mass-Energy Equivalence
Energy E is the function of mass m, and speed of light c which can be numerically expressed as 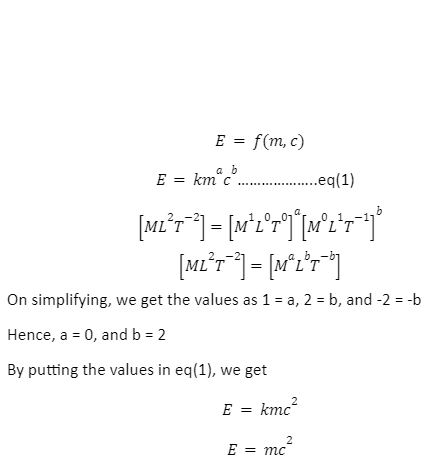
This is the numerically expressed relationship among Energy, mass, and speed of light.
Example 3: Vibration in string
Vibration of string v is the function of length of string L, linear mass density of that string M, and Tension in the string T which can be numerically expressed as:
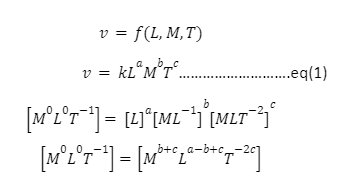
On simplifying, we get the values as 0 = b + c, 0 = a – b + c, and -1 = -2c
Hence, a = -1, b = -1/2, and c = 1/2
By putting the values in eq(1), we get
This is the numerically expressed relationship among vibration of string, length of string, linear mass density of the string, and Tension in the string.
Conclusion
We can conclude the key takeaways by stating that for deducing the relation among physical quantities, the application of dimensional analysis or principle of homogeneity is made. This article inculcates the capability among the students to identify and form the relationship among the physical quantities like mass, length, volume, time, temperature, gravity, speed, distance, and many more.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out











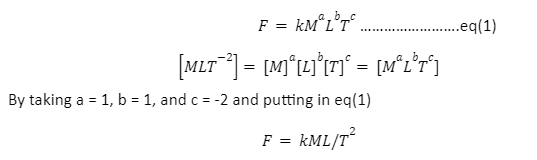 Concepts Used
Concepts Used