Physics defines radius of gyration as a different way of representing the distribution of area away from an axis that incorporates the effects of moments of inertia and cross-sectional area. When applied in polymer physics, the radius of gyration is used to define the dimensions of a polymer chain.
Let’s understand how mathematics explains the radius of gyration.
It is the root mean square (square root of the arithmetic mean of the squares of a set of numbers) distance of the particles of the object from either the centre of mass or the axis of rotation, depending upon the relevance of application, which we will learn in this article further.
Mathematical Derivation
Suppose an object has n particles with a uniform mass, say m. And, d₁, d₂…….dₙ are the perpendicular distances from the axis.
Now, the Inertia (I) would be calculated as –
I = m (d₁² + d₂² + d₃² + d₄² +………………dₙ²)
M being the total masses of the body which can be represented as m = M/n
I = M(d₁² + d₂² + d₃² + d₄² +………………dₙ²) /n
Now, we know by definition that I = M R²𝑔, where M is the total mass, and R²𝑔 is the radius of gyration of a body.
M R²𝑔 = M(d₁² + d₂² + d₃² + d₄² +………………dₙ²) /n
So, the radius of gyration formula will be –
R²𝑔 = (d₁² + d₂² + d₃² + d₄² +………………dₙ²) /n
So, in this way it can also be a measure from which the mass of a rotating rigid body is distributed about its axis of rotation.
Lets see its various applications-
Application in Mechanics
Here, the radius of gyration can be calculated in terms of the mass moment of inertia (Iₐ) about the given axis.
R²𝑔 = Iₐ/ M
M being the total mass
R𝑔 = √Iₐ/ M
This is the radius of the gyration formula for mass moment of inertia. Here, The rotating object’s mass is M, and the moment of inertia about any axis of revolution is I.
Application in Structural Engineering
In structural engineering, the two-dimensional radius of gyration is used to describe the distribution of cross-sectional area in a column around its centroidal axis in proportion to the mass of the body.
R²𝑔 = Iₐ/ A
R𝑔 =√ Iₐ/A
Where I is the area moment of Inertia, which is a characteristic that describes its deflection under load and is also called the second moment of area while A is the total cross sectional area.
The radius of gyration is the bending resistance of a cross section of any material. This occurs in pipes when the pipe’s walls produce the stress required to resist deformation, either elastically or plastically.
The radius of gyration is useful in estimating the stiffness of a beam and is usually calculated as an integral where the continuous bodies of matter are generally the objects of study.
Application in Polymer Physics
As mentioned earlier, the radius of gyration is used to define the dimensions of a polymer chain. But let’s see how it really works.

It can also be calculated by taking the sum of principal moments of the gyration tensor which is the algebraic object that describes the second moments of position of a collection of particles.
The radius of gyration is measured as an average over time, where {} denotes the average.
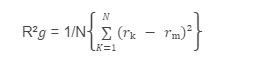
In theta circumstances, a polymer chain takes a walk in three dimensions, and the radius of gyration for this example can be determined as follows:
R𝑔 = 1√6 * √ N a
Where aN represents the contour length, which is the product of the number of segments of polymer molecule and its length.
The radius of gyration is a fascinating feature since it can be measured experimentally using static light scattering, as well as small angle neutrons and x-ray scattering. Theoretical polymer physicists may now compare their models to reality. Size exclusion chromatography can be used to estimate the hydrodynamic radius, which is numerically similar.
Application in geographical data analysis
The radius of gyration is used in data analysis to calculate a variety of statistics, including the spread of geographical locations. These locations gathered from social media users in order to look into a user’s regular mentions. This can be beneficial in determining how a specific set of social media users uses the site.
Conclusion
From the above explanation, we have learnt that the radius of gyration is different for different applications. In conclusion,the inertia of a body or an item in translational motion is solely determined by the mass of the body. The moment of inertia in rotational motion is determined by two elements – mass of the body and the effective distance between the axis of rotation and its particles.
In short, the moment of inertia depends on the mass distribution about the axis of rotation and so the radius of gyration can be ascertained about the axis of rotation of the body.
Irrespective of any shape of the body, The entire mass of the body can be assumed to be concentrated at a distance from the axis of rotation, and its moment of inertia about that axis stays unchanged.
And, this radial distance from a particular axis of rotation is the radius of gyration of a body rotating about that axis, and the square of radius of gyration multiplied by the total mass of the body gives the moment of inertia of the body about that axis.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out













