Watch Free Classes

Self Inductance And Mutual Inductance Problems: 

The concept of electromagnetic induction can be defined as the change in the magnetic field when the conductor is moved. It leads to the creation of voltage along the magnetic field. This rule was discovered by Michael Faraday. The concept of self Inductance and mutual inductance problems is used to make generators and motors. 

Resistance: 

When a component opposes a flow of current, it is known as resistance. A conductor can resist the current flow of electricity. 

Capacitor: 

A capacitor is a device that can store energy and charge. Capacitance is the power of a capacitor to reserve a charge. 

Inductor: 

An inductor is a device that resists the change in current flowing through a magnetic field. 

Mutual Inductance Example Problems: 

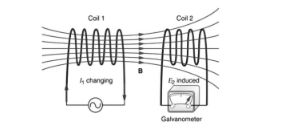
While explaining the concept of mutual Inductance circuit problems, one of the coils is given current while the other one is put on the electromotive force. 

Coil 1 has a supply and a rheostat 

Coil 2 is connected to a galvanometer 

There will be a flow of fluctuating current in coil 1. It will begin to face a shifting magnetic flux. This will also reflect on coil 2. This magnetic flux will have an impact on coil 2 and its EMF, which will lead to an opposite flow of current. Current flowing through coil 1 will cause a flux in coil 2. 

Practical Uses Of Mutual Inductance Example Problems: 

  • Inductors are used in choking circuits. 
  • Transformers use the concept of mutual Inductance circuit problems.
  • This concept is used for the preservation of energy. 
  • This concept is also applied in power converters. 

Mutual Inductance Example Problems: 

  • Find the self Inductance of a coil when the current of 2mA is passed with 100 turns and a magnetic flux of 0.2Wb.

Answer- current passing through the coil = l = 2mA 

Number of turns (N) = 100 

Magnetic flux = (ϕ)=0.2Wb

Self Inductance is calculated by = 

L=Nϕ/I

By putting in the values 

L=100×0.2/0.002

L=10000H 

Therefore, the coil has a self-inductance of 104H 

  • Two coils with self inductances 75mH and 55mH are placed as such so that 75% of the first coil is placed upon the second coil. Find the total mutual Inductance of these coils.

Answer-

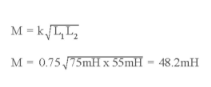
  • The mutual inductance of two coils is known to be 1.5H. self inductances of two coils are 5H and 4H. Find out their coupling coefficient.

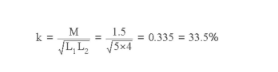
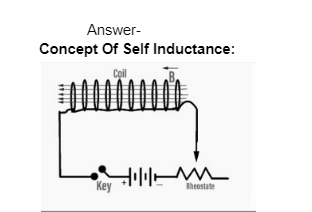
The rheostat produces a constant current in the coil. The magnetic field is also kept constant. When there is a change in the current of the rheostat, the current flowing through the coil will also change. Change in the current would also lead to a change in the magnetic flux. This will lead to the inducement of an EMF inside the coil. This will lead to a change in the direction of the current from where it is supplied. 

The current flowing through the coil is denoted as- 

ϕ ∝ I

Self-inductance is calculated as- 

L=ϕ/I

The Number of turns of the coil is denoted as- 

L=Nϕ/I

Nϕ=LI

Using time as a differentiator 

d/dt (Nϕ)=d/dt (LI)

N dϕ/dt=L dI/dt 

EMF according to Faraday’s law- 

 ε=–N dϕ/dt

The sign of subtraction in front of the equation signifies the opposite flow of energy. 

ε=–L dI/dt

L=–ε /(dI/dt) 

Magnetic Energy In A Conductor- 

The Rate of current in a circuit may be denoted as- 

dW/dt=ε I

Induced EMF of the coil is denoted as- 

dW/dt=–L dI/dt I

dW=–LI dI

Hence, we get 

∫dW=∫–LI dI

W=–( LI²)/2

Energy stored in the conductor is- 

U = (½) LI² 

Conclusion: 

Mutual Inductance example problems are used in the production of generators, motors, and transformers. The basic concept indicates that when a current is generated within a coil, it creates a voltage in the second coil. When the two coils are placed closely together, the magnetic energy of one coil links with another. It leads to the creation of voltage in the second coil. The ability of a coil to generate a voltage in another coil is known as mutual inductance.