Profile
Settings
Refer your friends
Sign out
A uniform thin rod is one where the linear mass density/Â mass per length of the rod, is the same at all locations along its length. A uniform rod’s centre of mass is located in the middle of the rod. If we assume a rod with a mass of M and a length of L, with a linear density of M/L, the rod depicts two moments of inertia depending on the location of the axis of rotation. Firstly, when the axis slices perpendicular through the rod’s centre of mass, exactly in the middle and secondly when the axis is positioned perpendicular at one of its two ends. In this article, we will learn to calculate the moment of inertia of a rod using both methods including the parallel axis theorem.Â
When an object of a specific mass is thrust into movement or brought to a standstill by an externally applied force, inertia is generated which is the opposition/resistance it gives. The tendency of substances to resist change/ inertia, changes with their mass. When compared to lighter items, heavier objects are more challenging to accelerate/propel while at rest and just as harder to halt when in motion.
In physics, the prefix ‘moment of’ denotes the rotational side of a linear quantity. For linear motion, the ‘moment of inertia’ is the rotational counterpart of mass. The letter ‘I’ stands for it.Â
A uniform thin rod is one where the linear mass density/Â mass per length of the rod is the same at all locations along its length. A uniform rod’s centre of mass is located in the middle of the rod.
Moment of inertia of a Rod
Assume a rod with a mass of M and a length of L, with a linear density of M/L. The rod depicts two moments depending on the location of the axis of rotation: whenÂ
- The axis slices perpendicular through the rod’s centre of mass, exactly in the middle.Â
- When the axis is positioned perpendicular at one of its two ends.
Axis passing through the mass centre
Imagine a minuscule component of length dl matching to the minuscule component of mass dm. We would like a thin rod so that we may suppose it has a tiny cross-sectional area and it can be conceived of as a string of masses strung across a one-dimensional single direction. For simplicity, the rotating axis is perpendicular to the rod and goes through the midway in this case. When we draw the origin at the centre of mass on the axis line, we see that the length from the beginning to the rod’s end on the left is -L/2, whereas the length from the beginning to the other end on the right is +L/2.
 If the rod is uniform,
The linear density stays constant in a way that:
λ= M / L = dm / dl
or
dm = M / L *dl
We may compute the moment of inertia by replacing the value of dm in our formula.
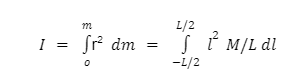
The limitations have altered from the previous indicated M to a necessary fraction of L since the variable of integration is length (dl).
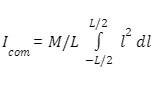
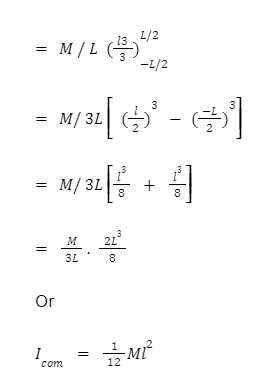
Axis through an end
Draw the beginning at one end of the axis to compute the moment of inertia of a rod whenever the axis is at one of its ends.
We must utilise the same expression this time, but with a different limit.The limit about which we integrate is zero to L since the axis stops at the opposite end.
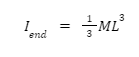
We may get the identical conclusion for the moment of inertia of rod about the end by employing the parallel axis theorem.The striking resemblance between the processes of determining the moment of inertia of a rod for an axis through its middle and an axis through its end implies that there may be a simplified way to determine the moment of inertia of a rod about every axis parallel to the axis through its centre of mass.The parallel axis theorem is expressed as:
Conclusion
The resistance to change (inertia) of substances varies with their weight. The linear mass density/mass per length of the rod is the same at all points along its length in a homogeneous thin rod. The moment of inertia is computed by two methods, when the axis cuts perpendicular across the rod’s centre of mass, exactly in the middle and when the axis is perpendicular at one of its two ends. We’ve also discussed parallel axis theorem in this article.
