A moment of inertia also referred as MOI is a measurable statistic of a body’s angular momentum or the response that the object exhibits when its speed of rotation around an axis is changed by the application of some torque. The axis might be in the interior or exterior, may be permanent or not.
The MOI, on the other hand, is often defined on that axis and characterized as the total of the products produced by the multiplication of the masses within each component or particle of substance in a specific object by its distance square from the axis of rotation.
Speaking about the hollow cone’s moment of inertia. It is symmetrical about its axis, and for this, the formula for moment of inertia of a circular hollow cone is given in the below equation.
I=MR² ⁄ 2
Where,
M = mass of the hollow cone
R = distance from the axis of rotation or radius from the axis of rotation
I = Moment of inertia of the hollow cone
The derivation of this hollow cone is done by taking a small element of a circular ring inside the cone. Similar to the method used in a solid cone where a disc is used and here we are using a circular ring because here the cone is hollow. So, we are going to find the moment of inertia of that small elemental ring using the base formula and we’re gonna integrate the moment of inertia having some limitations and find out the moment of inertia of the complete hollow cone.
In this article, we are going to explain the derivation for finding out the moment of inertia of a hollow cone using the integration method in the coming paragraphs.
Derivation
Initially let us discuss the elements and attributes used in deriving the formula for the
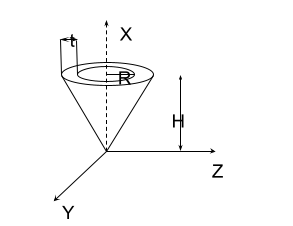
MOI of a hollow cylinder. Refer to the below diagram for the same.
As per the diagram above, consider a hollow cone having a thickness of t and height of H. Also consider the radius of the cone to be R. For the elemental ring, consider the thickness of the ring to be at a slant height of x, with the radius r and the thickness dl having mass as dm.
To begin with using the similarity of the triangle we can have the radius of the cone to be as,

Now, we’ve got the mass and the distance from the axis of rotation of the ring. So, we’ll introduce the same into the basic equation of moment of inertia which is,
I=M ×R²
So, the equation becomes,
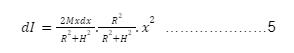
Here, equation 5 denotes the moment of inertia of the ring.
At last, as we said earlier we’re going to integrate equation 5 to find out the moment of inertia of the complete hollow cone.
So, integrating the same as,
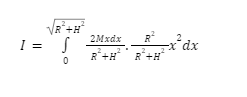
Rewriting it as,

Conclusion
To sum up, similar to the derivation of a solid cylinder, we’ve initially taken a small elemental ring having some thickness and at a slant height of some particular value. Initially, we need to find the moment of inertia of that small elemental ring using the base formula which is the product of the mass of the ring and the distance’s square from the rotational axis. And then integrating the same MOI found from the ring having limits as zero and the slant height of the cone we will find the required formula for the moment of inertia of the hollow cone.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out













